MODELLO DI FRIEDMANN

IL MODELLO DI FRIEDMANN

( fonte principale: Karttunen et. al. Fundamental Astronomy - Springer)

IL MODELLO DI FRIEDMANN. Allo scopo di derrminare la precisa dipendenza dal tempo del fattore di scala R(t) è necessaria una teoria della gravità. Nel 1917 A. Einstein presentò un modello di universo basato sulla Teoria Generale della Relatività. In questa teoria è descritto uno spazio geometrico simmetrico con un volume finito e senza confini. In accordanza con principio cosmologico, il modello era omogeneo e isotropo. Era anche statico: il volume nello spazio non cambiava. Allo scopo di ottenere il modello statico, Einstein ha dovuto introdurre una nuova forza repulsiva, il termine cosmologico, nelle sue equazioni. La grandezza di questo termine cosmologico è dato dalla costante cosmologica Λ. . Einstein presentò il suo modello prima che il redshift delle galassie fosse conosciuto e allora parlare di un Universo statico era ragionevole. Quando è stata scoperta l'espansione dell'Universo, questo argomento in favore della costante cosmologica svanì. Einstein stesso successivamente chiamò questo il più grande errore della sua vita. Tuttavia le più recenti osservazioni sembrano ora indicare che occorre considerare una costante cosmologica diverza da zero.

Il fisico di S. Pietroburgo A. Friedmann e successivamente e indipendemente il belga G. Lemaitre studiarono le soluzioni cosmologiche delle equazioni di Eintsein. Secondo Friedmann, posto Λ = 0, è possibile un modello di Universo che si evolve, o in espansione o in contrazione. Dal modello di Friedmann possono essere derivate formule esatte per il redshift e la Legge di Hubble. È interessante che l'esistenza di tre tipi di modelli (statico, in espansione e in contrazione) e le loro leggi possono essere derivate da considerazioni puramente Newtoniane con risultato di un completo accordo con la trattazione relativistica.

Adesso consideriamo una piccola regione sferica che si espande nell'universo. In una distribuzione sferica della materia la forza gravitazionale in un dato guscio sferico dipende solo dalla massa all'interno il guscio. Qui si assumerà che Λ=0. Ora consideriamo il moto di una galassia di massa m alla fine di una regione sferica dell'Universo. In accordanza con la Legge di Hubble la velocità sarà v=H·r e la corrispondente energia cinetica $K = \frac{1}{2} m v^{2}$ . L'energia potenziale alla fine della sfera di Universo di massa M è $U = - \frac{GMm}{r}$ , allora l'energia totale è $E = K + U = \frac{1}{2} m v^{2} - G \frac{mM}{r}$ che deve essere costante. Se la densità media dell'Universo è ρ, la massa dell'Universo è $M = \frac{4}{3} π r^{3} ρ$ . Il valore di ρ_c che corrisponde a E=0 è chiamato densità critica.

Per ricavare la densità critica si pone:

$E = \frac{1}{2} m H^{2} r^{2} - G \frac{mM}{r} = \frac{1}{2} m H^{2} r^{2} - Gm \cdot \frac{4}{3} π r^{3} . \frac{ρ_{c}}{r} = m r^{2} (\frac{1}{2} H^{2} - \frac{4}{3} πG ρ_{c}) = 0$

da cui $ρ_{c} = \frac{3 H^{2}}{8 πG}$ .


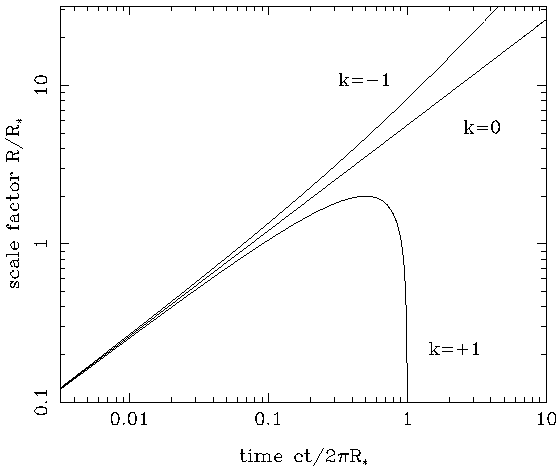
L'espansione dell'Universo può essere paragonata al moto di una massa lanciata verticalmente dalla superficie di un corpo celeste. La forma dell'orbita dipende dall'energia iniziale. Allo scopo di calcolare l'orbita completa devono essere note la massa M del corpo principale e la velocità iniziale. In cosmologia, i corrispondenti parametri sono la densità media e la costante di Hubble. Il modello con E=0 corrisponde con il modello euclideo di Friedmann, detto modello di Einstein-de Sitter. Se la densità supera la densità critica, l'espansione di qualsiasi regione sferica cambierà in contrazione e vi sarà il collasso in un punto. Questo corrisponde al modello chiuso di Friedmann. Infine se ρ<ρ₀ si ottiene il modello iperbolico sempre in espansione. Il comportamento del fattore di scala in questi tre casi è mostrato in figura. Questi tre modelli dell'univrso sono chiamati i modelli standard. Loro sono i più semplici modelli cosmologici relativistici con Λ=0. Modelli con Λ≠0 sono matematicamente più complicati, ma mostrano lo stesso comportamento generale Il trattamento newtoniano, più semplice, del problema dell'espansione dell'Universo è possibile perchè la meccanica newtoniana è approssimativamente valida in piccole regioni dell'Universo. Tuttavia, sebbene le equazioni risultanti sono formalmente simili, l'interpretazione delle quantità coinvolte (per esempio il parametro k) non è lo stesso come ne contesto relativistico. La geometria globale del modello di Friedmann può solo essere capita entro la Teoria della Relatività Generale .

Consideriamo due punti separati da una distanza r. Sia V la loro velocità relativa.
Si ha che: $r = \frac{R (t)}{R (t_{0})} \cdot r_{0}$ e $V = \dot{r} = \frac{\dot{R} (t)}{R (t_{0})} \cdot r_{0}$ e allora la costante di Hubble è $H = \frac{v}{r} = \frac{\dot{R} (t)}{R (t)}$ .
La decelerazione dell'espansione è descritta dal parametro di decelerazione q, definito come $q = - \frac{R \overset{. .}{R}}{{\dot{R}}^{2}}$ .
Il parametro di decelerazione descrive la variazione del tasso di espansione $\dot{R}$ . Il fattore addizionale è stato incluso allo scopo di farlo adimensionale ovvero indipendente dalla scelta delle unità dimisura della lunghezza e del tempo.

Il valore del parametro di decelerazione può essere espresso in termini della densità media. Il parametro di densità Ω è definnito come $Ω = \frac{ρ}{ρ_{0}}$ in modo tale che Ω=1 corrisponde al modello di Einstein-Sitter. Dalla conservazione della massa segue che $ρ_{0} R_{0}^{3} = ρ R^{3}$ .
Usando l'espressione ricavata precedentemente per la densità critica si ottiene: $Ω = \frac{8 πG}{3} \cdot \frac{ρ_{0} R_{0}^{3}}{R^{3} H^{2}}$ .
D'altro canto q può essere scritta: $q = \frac{4 πG}{3} \cdot \frac{ρ_{0} R_{0}^{3}}{R^{3} H^{2}}$ .
Allora vi è una relazione semplice tra Ω e q: Ω= 2q . Il valopre di q=½ del parametro di decelerazione corrisponde alla densità critica Ω=1. Ambedue le quantità sono di uso comune in cosmologia. Dovrebe essere notato che la densità e la decelerazione possono essere osservate indipendentemnente. La validità della precedente equazione è allora un test per la correttezza della relatività generale con Λ=0.