EQUILIBRIO INTERNO DELLE STELLE

LE CONDIZIONI PER L'EQUILIBRIO INTERNO

( fonte principale: Karttunen et. al. Fundamental Astronomy - Springer)


Le condizioni per l'equilibrio interno delle stelle sono determinate da quattro equazioni differenziali: l'equazione dell'equilibrio idrostatico, l'equazione di continuità della distribuzione della massa , l'equazione di produzione dell'energia, l'equazione di gradiente di temperatura.
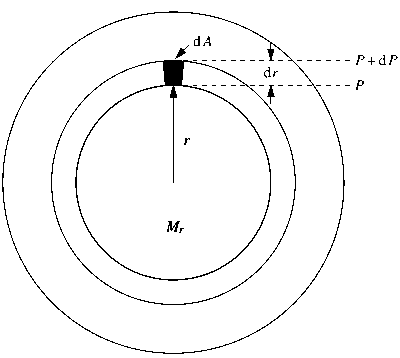
EQUAZIONE DELL'EQUILIBRIO IDROSTATICO. La forza di gravità attrae il materiale stellare verso il centro. A questa attrazione fa contrasto la pressione dovuta al moto di agitazione termica. La prima condizione per l'equilibrio interno è proprio legata all'equilibrio di queste due forze contrastanti. Consideriamo un elemento di volume cilindrico a distanza r dal centro della stella. Il volume è dV= dA·dr, con dA la base e dr l'altezza. La massa dell'elemento è dm= ρ(r)·dAdr con ρ(r) la densità nella posizione r (si suppone una simmetria sferica). Se la massa entro il raggio r è M_r, la forza gravitazionale verso l'interno nell'elemento di volume considerato è: $d F_{g} = - \frac{G M_{r} dm}{r_{2}} = - \frac{G M_{r} ρ (r)}{r^{2}} dAdr$ Se la pressione nella superficie sferica inferiore è P e quella sulla superficie sferica superiore P+dP, la forza verso l'esterno dovuta alla pressione è: $d F_{p} = PdA - (P + dP) dA = - dPdA$ In condizioni di equilibrio: $d F_{g} + d F_{p} = 0 \to - \frac{G M_{r} ρ (r)}{r^{2}} dAdr - dPdA = 0 \to \frac{dP}{dr} = - \frac{G M_{r}}{r^{2}} ρ (r)$ Questa è l'equazione dell'equilibrio idrostatico.
EQUAZIONE DI CONTINUITÀ DELLA DISTRIBUZIONE DELLA MASSA. La seconda equazione ipotizza una distribuzione di masse che, anche se può dipendere dalla distanza dal centro, ha comunque una simmetria sferica. Se consideriamo un guscio sferico di spessore dr la sua massa è: $d M_{r} = 4 π r^{2} ρ (r) dr \to \frac{d M_{r}}{dr} = 4 π r^{2} ρ (r)$ Questa è l'equazione di continuità della distribuzione della massa
EQUAZIONE DI PRODUZIONE DELL'ENERGIA. La terza equazione esprime la conservazione dell'energia. Ovvero che l'energia prodotta nella stella verrà irradiata all'esterno. Se si considera di nuovo un guscio sferico di spessore dr e massa dM_r, sia L_r il flusso di energia (potenza) che è trasmessa attraverso la superficie inferiore e L_r+dr quello trasmesso attraverso la superficie superiore. Il flusso netto è: $d L_{r} = L_{r + dr} - L_{r} = ε \cdot d M_{r} = ε \cdot 4 π r^{2} ρ (r) dr \to \frac{d L_{r}}{dr} = 4 π r^{2} ρ (r)$ ε è il coefficiente di produzione di energia (energia trasmessa per unità di tempo e unità di massa). Questa è l'equazione di produzione di energia.
EQUAZIONE DI GRADIENTE DELLA TEMPERATURA. La quarta equazione dà la variazione della temperatura in funzione del raggio. La forma dell'equazione dipende dal meccanismo di trasporto dell'energia (conduzione, convezione o radiazione). I processi più comuni per il trasporto dell'energia sono: internamente convezione, esternamente radiazione. Se si instaura un equilibrio radiativo l'energia prodotta all'interno è trasportata interamente all'esterno mediante radiazione. È possibile costruire un modello di equilibrio radiativo rappresentato dall'equazione differenziale (equazione del gradiente di temperatura) : $\frac{dT}{dr} = (- \frac{3}{4 a c}) (\frac{κρ (r)}{T^{3}}) (\frac{L_{r}}{4 π r^{2}})$ dove a= 4σ/c= 7.564·10^-16 Jm^-3K^-4 è la costante di radiazione, c la velocità della luce e ρ(r) la densità. Il coefficiente di assorbimento di massa κ fornisce l'assorbimento di energia per unità di massa. Il suo valore dipende dalla temperatura, dalla densità e dalla composizione chimica della stella.
LE CONDIZIONI AL CONTORNO. Per poter risolvere le quattro equazioni differenziali occorre conoscere delle costanti di integrazione dette condizioni al contorno. Le più ovvie sono: Non ci sono sorgenti di energia o masse entro il raggio r=0. Quindi M₀=0 e L_r=0 La massa totale entro un raggio R (raggio totale) è nota M_R= M La temperatura e la pressione sulla superficie della stella hanno un valore noto: T_R e P_R. Inoltre i loro valori sono spesso trascurabile in confronto alle temperature e alle pressioni all'interno della stella. Comunque si dimostra che le condizioni per l'equilibrio interno della stella sono determinate se è nota la massa e la composizione chimica della stella. Questo risultato è noto come teorema di Vogt-Russel