Le quantità nU e nL rappresentano le popolazioni dei due livelli. Poichè gli atomi possono essere nello stato U o nello stato L allora nU + nL = n sarà una quantità costante e rappresenta il numero totale di atomi per unità di volume.
È evidente che se c'è una variazione nelle popolazioni deve essere: (aumento dell'una uguale alla diminuizione dell'altra).
Si ci può aspettare che il numero degli atomi che dal livello U passano al livello L (la diminuizione) è proporzionale alla popolazione del livello U: o anche che . Il coefficiente AUL è detto coefficiente di Einstein.
La soluzione dell'equazione differenziale è con nU(0) la popolazione del livello U al tempo t=0. τu= 1/AUL è il tempo necessario perchè la popolazione dello stato U diminuisca di un fattore 1/e (circa 37%) rispetto al valore iniziale (con solo il meccanismo dell'emissione spontanea l'unica possibilità sono le transizioni U→ L). Per le transizioni nell'atomo di idrogeno τU≃ 10-8÷10-4 s. L'atomo di idrogeno per emissione spontanea torna allo stato fondamentale rapidamente.
Anche in questo caso la diminuizione temporale della popolazione è proporzionale alla popolazione iniziale ma la costante di proporzionalità (coefficiente di Einstein) sarà legata all'intensità della radiazione incidente (più è elevata l'intensità e più è alta la probabilità che avvenga una emissione stimolata).
In questo caso l'equazione differenziale della popolazione nel livello U è:
Iν è l'intensita monocromatica della radiazione. La soluzione dell'equazione differenziale è:
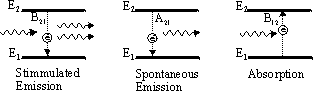
In questo caso la transizione sarà favorita non solo dall'intensità della radiazione incidente ma anche dalla abbondanza di atomi nello stato L. Bisogna quindi riferirsi allo stato L e la soluzione dell'equazione differenziale che ne consegue è del tipo:
Il coefficiente BLU non è in generale uguale a BUL.
Come detto prima il numero totale di atomi nel livello U o L è costante, da cui :
E si arriva alla condizione detta di detailed balance:
il cui significato è che la variazione totale degli atomi nel livello U è dovuta alla emissione spontanea o indotta (diminuizione) sommata ad assorbimento della radiazione (aumento).