DISTANZE, MASSA E LUMINOSITÀ DELLE GALASSIE

( fonte principale: Karttunen et. al. Fundamental Astronomy - Springer)

LE DISTANZE DELLE GALASSIE. Possiamo determinare la luminosità assoluta, le dimensioni lineari e le masse delle galassie se riusciamo a misurare le loro distanze da noi. Per le galassie nel Gruppo Locale (nome dato al gruppo di galassie di diametro 3 Mpc, di cui fa parte anche la nostra galassia, che comprende più di 70 galassie, per la maggior parte, escluso Andromeda, di piccole dimensioni), le distanze possono essere determinate mediante le stelle variabili che riusciamo ad osservare . A scale più grandi (oltre 50 Mpc) possiamo stimare le distanze sulla base dell'espansione dell'Universo. Per connettere le misure di queste due regioni è necessaria una determinazione indipendente delle distanze basate su proprietà di particolari galassie. In certi casi possiamo determinare le distanze per mezzo di componenti strutturali delle galassie, come le dimensioni delle regioni H II o le magnitudini degli ammassi globulari.

Tuttavia per distanze oltre 10 Mpc, per misurare la luminosità assoluta delle galassie, occorrono metodi che non dipendono dal dover conoscere le distanze. Sono stati proposti diversi metodi. Per esempio S. van den Berg ha introdotto una classificazione della luminosità delle galassie a spirale basandosi sulla correlazione tra la luminosità e la sporgenza delle spirali. Possiamo ottenere altri indicatori per la misura delle distanze da alcune proprietà intrinseche delle galassie che sono correlate direttamente con la luminosità totale (e poi, nota la luminosità, ricaviamo le distanze). Queste proprietà sono il colore, la brillanza superficiale, e le velocità interne alle galassie.

Per esempio la luminosità assoluta di una galassia dipende dalla sua massa. Questa, a sua volta, è legata alle velocità delle stelle e del gas all'interno della galassia. Quindi si può trovare una relazione tra luminosità assoluta e dispersione delle velocità (per le ellittiche) e velocità rotazionali (per quelle a spirali). E siccome le velocità rotazionali possono essere misurate con precisione mediante la larghezza della linea dell'idrogeno a 21 cm allora si può ricavare la luminosità assoluta e poi attraverso di questa stimare la distanza. Infine si è scoperto che la luminosità delle galassie brillanti negli ammassi è con buona approssimazione, costante. Questo fatto può essere usato per misurare distanze ancora più grandi e fornisce informazioni molto importanti per la cosmologia.
LA LUMINOSITÀ DELLE GALASSIE. La definizione di luminosità totale di una galassia non è univoca perchè le galassie non hanno confini netti. Una convenzione è misurare la luminosità di una galassia fino non oltre 26.5 mag/arcsec quadrati. Per studiare la distribuzione delle galassie nell'universo, viene definita una grandezza fisica detta funzione di luminosità Φ(L) che fornisce il numero di galassie per unità di volume con un determinato intervallo di luminosità. 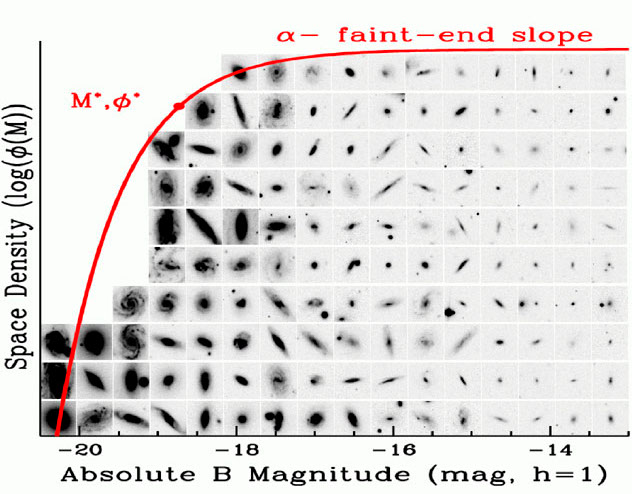Dallo studio delle osservazioni si è ricavata una curva che approssima i dati detta funzione di luminosità di Schechter .
Dal grafico, che riporta logaritmo della funzione di luminosità in funzione della magnitudine assoluta e la funzione di Schechter, si vede che sono poche le galassie con una elevata luminosità, mentre le galassie con bassa luminosità tendono a distribuirsi in modo uniforme nell'Universo.

LA MASSA DELLE GALASSIE. Lo studio della distribuzione delle masse delle galassie è importante sia per la cosmologia sia per le teorie sull'evoluzione delle galassie. Per determinare la massa delle galassie principalmente si studia la velocità delle loro stelle e del gas interstellare ma anche si osserva il loro moto relativamente agli ammassi di galassie. Le misure sono solitamente presentate nella forma del rapporto M/L, detto rapporto massa-luminosità usando la massa solare e la luminosità solare come unità.

11

Ci sono diversi metodi per misurare la massa delle galassie.

Per le galassie ellittiche, che non sono dotate di una velocità angolare ordinata elevata, si misura la velocità di rotazione e la dispersione delle velocità misurabili dall’allargamento delle righe spettrali.
Per capire il significato fisico della dispersione delle velocità basti pensare che i moti caotici delle stelle, in quanto tali, non hanno una direzione privilegiata. In ogni punto di una certa galassia ellittica ci sono approssimativamente lo stesso numero di stelle che si muovono verso l'osservatore ed in direzione opposta (lungo la linea di vista dell'osservatore) rispetto ad una velocità locale media che ne rappresenta il moto rotatorio d'insieme. La composizione di questi moti genera una distribuzione quasi-gaussiana, il cui allargamento è una misura della dispersione delle velocità.
Nota la dispersione delle velocità e la velocità di rotazione, poichè le galassie sono sistemi in equilibrio, si può applicare il teorema del viriale, che fornisce un legame tra energia cinetica disordinata, misurata dalla dispersione della velocità , e l’energia potenziale di autogravitazione.
Si ricava che la massa può essere calcolata con la formula : M ≈ 2 · v 2 · R G , dove G è la costante di gravitazione universale, v rappresenta la dispersione di velocità.

Per le galassie a spirale si misura la curva di rotazione che dà la velocità di rotazione delle spirali in funzione del raggio. Poi la massa viene ricavata dalla condizione di equilibrio tra forza gravitazionale, che trattiene le stelle in orbita circolare, e la forza centrifuga: GM R 2 ≈ v rot 2 ( R ) R → M ≈ R · v rot 2 ( R ) G .
Un terzo metodo per misurare la massa delle galassie è osservare il suo moto relativamente ad un'altra, in modo simile a quanto si fa per le stelle binarie. Tuttavia poichè il periodo orbitale delle galassie è molto elevato, circa 1 miliardo di anni, si possono ottenere solo infomazioni statistiche con questo metodo.

Un quarto metodo è applicare il teorema del viriale ad ammassi di galassie assumendo che questo sia in equilibrio. L'energia cinetica si può calcolare con il redshift e l'energia potenziale dalla separazione spaziale tra le galassie nell'ammasso.

I risultati delle osservazioni e delle simulazioni indicano che se si considerano volumi nello spazio più grandi si ottengono più grandi valori del rapporto M/L. Questo significa che la massa aumenta più della luminosità. Da questi dati si evince che deve esistere una componente gravitazionale senza interazione elettromagnetica perchè, altrimenti, questa si rivelerebbe in effetti di assorbimento, come per il gas interstellare. Questo problema è conosciuto come il problema della massa mancante ed è una delle principali questioni non risolte dell'astronomia extragalattica.