- La precessione luni-solare
- La precessione planetaria
- Le nutazioni
- L'errore di parallasse
- L'errore di aberrazione
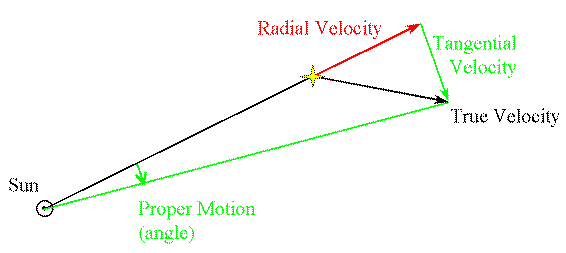
- L'errore per moti propri
LA PRECESSIONE LUNI-SOLARE. A
causa delle interazioni gravitazionali del Sole e della Luna con la
Terra, l'asse di rotazione della Terra, e quindi il piano equatoriale,
non è costante ma ha un lento moto di precessione
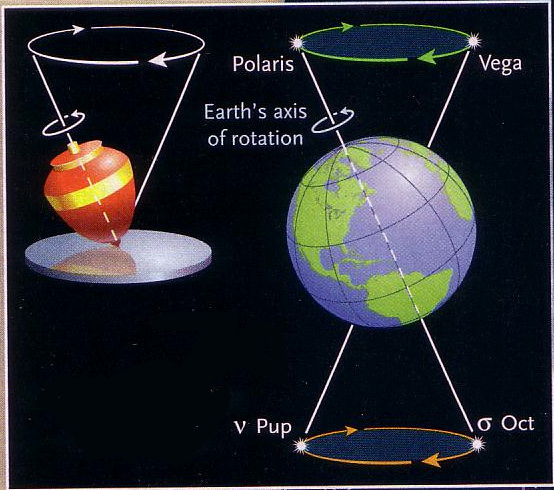
luni-solare (simile a quello di una trottola)
attorno il Polo Nord dell'eclittica con un periodo di circa 26000 anni.
Adesso il polo nord celeste è diretto approssimativamente verso Polaris
ma tra 12000 anni sarà diretto verso Vega.
Conseguenza della precessione è il moto del punto γ o vernale
lungo l'eclittica in senso orario di circa 50" ogni anno e la
variazione della longitudine eclittica di ogni corpo celeste (dato che
la longitudine eclittica è calcolata a partire dal punto γ). Non
cambia, in prima approssimazione, la latitudine eclittica (che dipende
dalla orientazione nello spazio del piano dell'eclittica).
Naturalmente, sempre a causa della precessione, variano anche le due
coordinate equatoriali ascensione retta e declinazione dato che varia
punto γ e orientazione del piano equatoriale.
Adesso deriviamo le espressioni delle variazioni o perturbazioni delle coordinate equatoriali.
Consideriamo le equazioni di trasformazione da eclittiche ad equatoriali (↑) :
E deriviamo l'ultima rispetto la longitudine eclittica λ (la latitudine eclittica e l'obliquità non dipendono da λ) :
Riprendiamo le equazioni di trasformazione da equatoriali ad eclittiche (↑):
Sostituendo la seconda troviamo: .
Ora consideriamo la seconda delle trasformazioni da equatoriali ad eclittiche e deriviamola sempre rispetto λ:
Ricaviamo sinα·cosδ·dα , sostituiamo il dδ trovato precedentemente e sostituiamo anche sinλ·cosβ con la prima equazione delle equazioni da equatoriali ad eclittiche:
Dividendo tutto con sinα·cosδ:
Quindi le perturbazioni o le variazione delle coordinate equatoriali per una perturbazione della longitudine eclittica ( circa 50" l'anno) sono:
Queste espressioni sono di solito scritte nella forma:
avendo posto m= cosε·dλ e n= sinε·dλ (costanti di precessione).
Queste formule ci forniscono le correzioni da apportare alle coordinate equatoriali della stella a causa della precessione lunisolare.
Tuttavia anche l'obliquità dell'eclittica ε varia lentamente nel tempo e quindi m ed n non sono rigorosamente costanti. Ma per tempi non molto lunghi ( < 10 anni) si possono considerare costanti.
LA PRECESSIONE PLANETARIA. Anche i pianeti, inoltre, hanno una loro influenza sulla Terra; essi influiscono sul movimento della Terra intorno al Sole, modificandolo e determinando uno spostamento del piano dell’orbita terrestre. Questo movimento è la precessione planetaria e fa si che si sposti nello spazio il polo dell’eclittica provocando come risultato che il movimento di precessione totale luni–solare e planetario sia un moto conico periodico, ma non chiuso. Ciò significa che l’asse terrestre, in 26.000 anni, compie un giro completo, ma non torna ad orientarsi esattamente nello stesso punto del cielo. A causa della precessione planetaria l'obliquità dell'eclittica ε varia di circa 0.47" l'anno. L’effetto di questa precessione è quindi di minore importanza rispetto alla precessione luni-solare
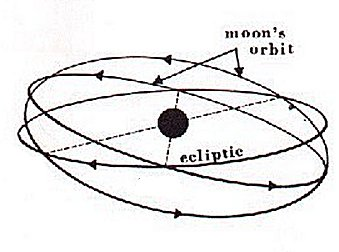
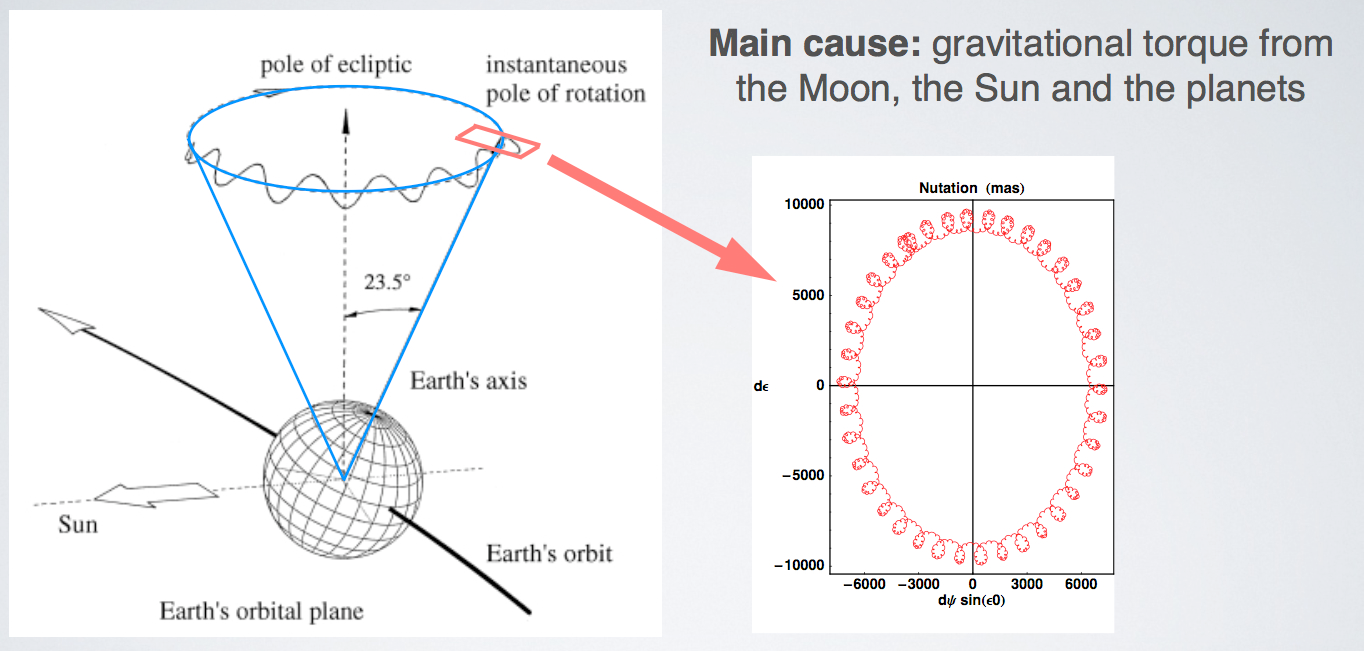
Questo effetto chiamato nutazioni dell'asse terrestre crea perturbazioni sia alla longitudine eclittica, quindi al punto γ, sia alla obliquità dell'eclittica ovvero l'angolo di inclinazione tra asse terrestre ed piano dell'eclittica. I calcoli di tale perturbazione sono complessi ma le perturbazioni per nutazioni non sono elevate , solo pochi secondi di arco.
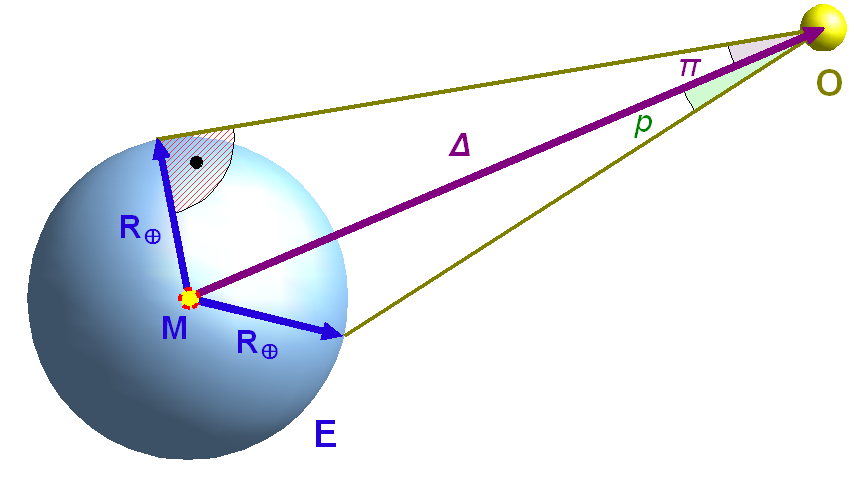
| PARALLASSE. La parallasse è la differenza di
coordinate dovuta alla diversa posizione della Terra (dovuta
alla rivoluzione terrestre). La perturbazione dovuta alla
parallasse è utilizzata per determinare la distanza delle
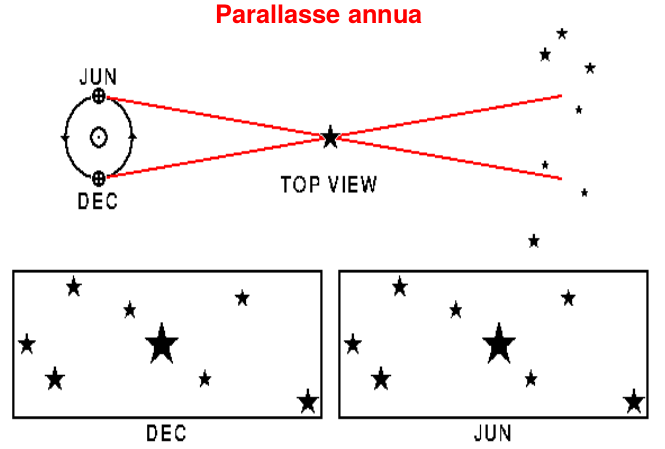
stelle più vicine. La parallasse annua è
l'angolo sotteso dal raggio dell'orbita terrestre (il raggio
medio dell'orbita terrestre è la unità astronomica AU). Per gli
oggetti del Sistema Solare le distanze sono determinate con la
parallasse diurna o orizzontale π che è
l'angolo sotteso dall'oggetto dal raggio equatoriale terrestre.
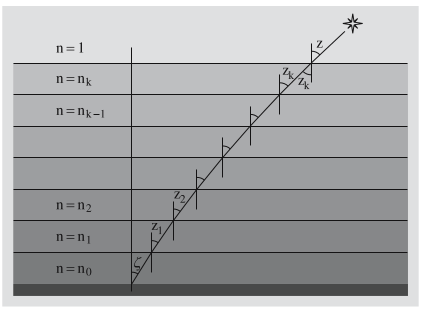
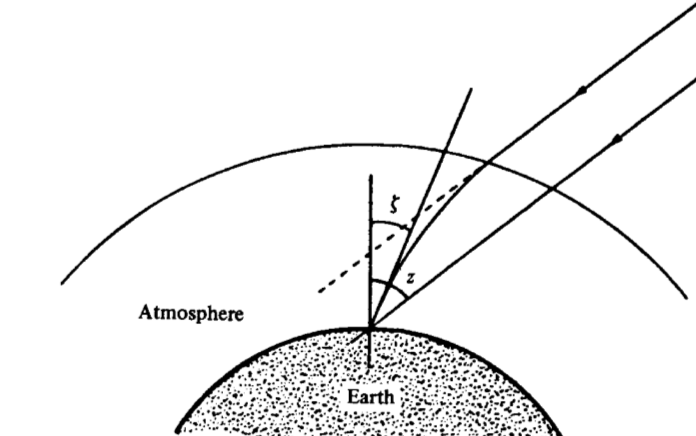
Per determinare la parallasse diuna occorre considerare lo
spostamento della diversa direzione apparente rispetto le
stelle fisse dell'oggetto quando è allo zenith e quando è
all'orizzonte. La parallasse diurna della Luna è circa 57' e
del Sole 8.79".
In astronomia il termine parallasse sta comunque ad indicare tutte quelle perturbazioni dovute alle diverse direzioni di osservazione degli oggetti celesti. |
 |
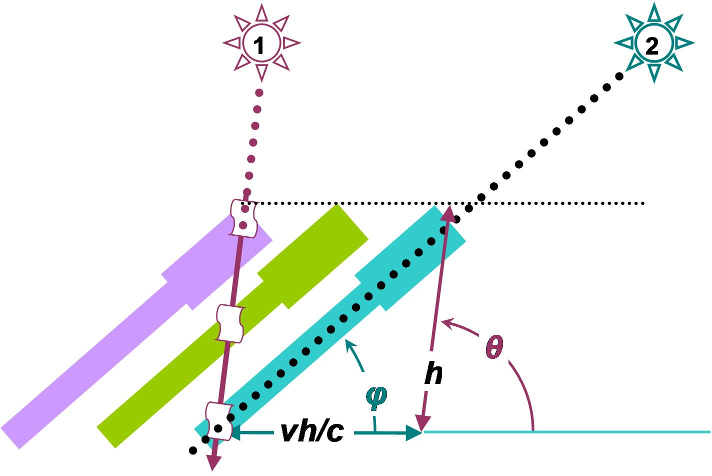
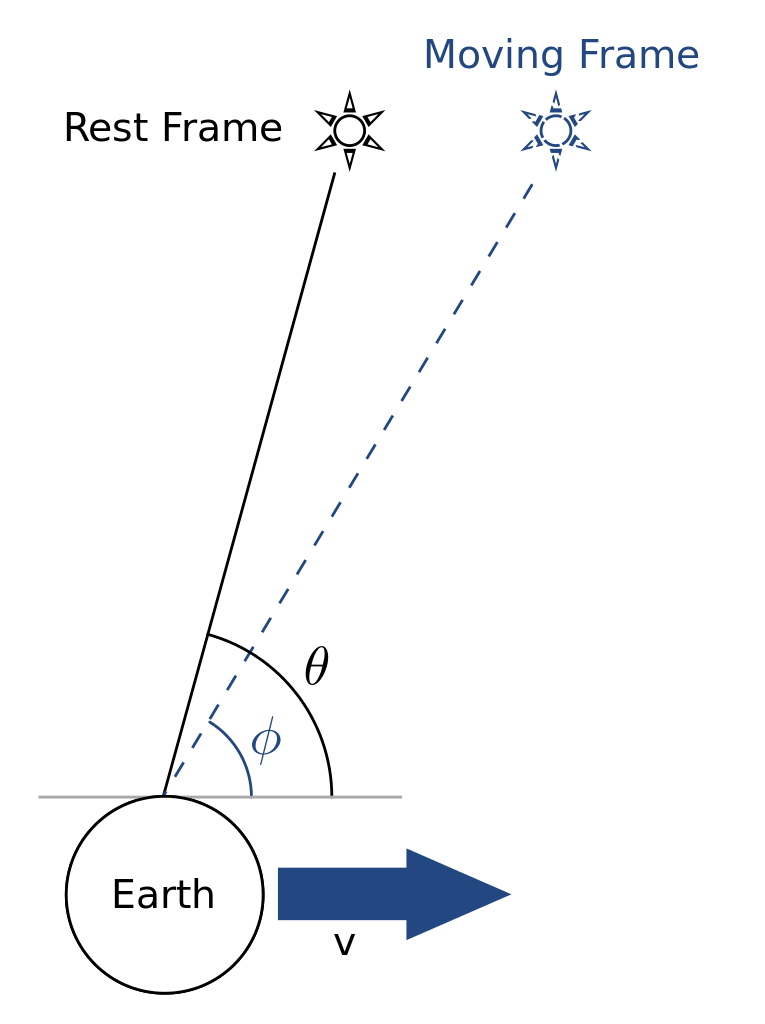
ABERRAZIONI. Poichè riceviamo informazioni dagli oggetti celesti dalla luce, e poichè la velocità della luce è finita, se siamo in moto osserviamo gli oggetti un pò spostati rispetto alla loro direzione osservata quando siamo fermi. La Terra è in moto nello spazio e quindi gli oggetti celesti sono visti un pò spostati a secondo la posizione della Terra al momento dell'osservazione. Dalla figura si vede che lo spostamento x è uguale : con l la lunghezza del telescopio, v la velocità dell'osservastore, c la velocità della luce, θ l'angolo tra la direzione vera dell'oggetto e la direzione della velocità dell'osservatore. Il cambio di direzione in radianti a (costante di aberrazione) è: La costante di abberrazione massima a causa del moto orbitale della Terra è di circa 21", e la costante di abberrazione massima dovuta al moto diurno di rotazione della Terra è di circa 0.3". |
 |
|
 |