TRIGONOMETRIA SFERICA

Una sfera è il luogo dei punti nello spazio cartesiano tridimensionale equidistante da un punto dato, detto centro. Ogni piano passante per il centro divide la sfera in due semisfere. L'intersezione di tale piano con la superficie sferica è una circonferenza detta circolo massimo o circolo equatoriale. La retta passante per il centro e normale a tale piano definisce due punti diametralmente opposti che sono i poli di tale cerchio equatoriale. Se una sfera è intersecata da un piano non passante per il centro l'intersezione è un circolo minore. Dati due punti Q e Q' sulla sfera esiste solo un circolo massimo a cui appartengono. L'arco QQ' del circolo massimo a cui appartengono Q e Q' è il cammino più breve che collega i due punti sulla sfera (geodesica).

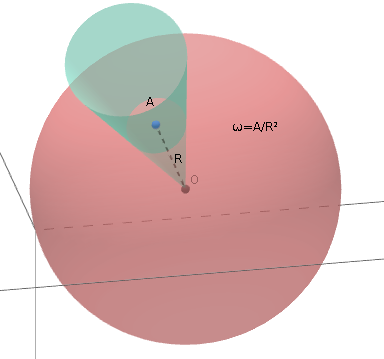
Si definisce angolo solido il rapporto tra la superficie intercettata su di una sfera di raggio R da un cono con vertice nel centro O della sfera e R². L’unità di misura dell’angolo solido è lo steradiante.

 1

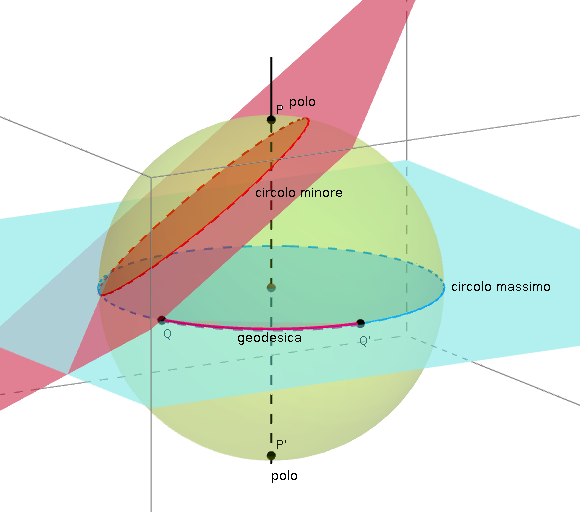
Un triangolo sferico è una figura qualunque a tre angoli che giace su una superficie sferica i cui lati sono archi di un circoli massimi.

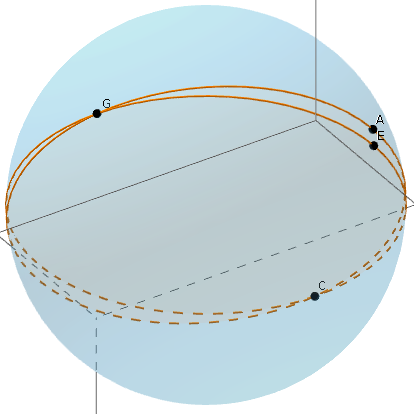
Per esempio il triangolo sferico di figura (in basso a destra) ha come lati i tre archi AB ︵ , BC ︵ e AC ︵ .

a ̂ , b ̂ e c ̂ (o semplicemente a, b e c) sono gli angoli al centro sottesi dai lati del triangolo sferico.

Le lunghezze degli archi sono:

AB ︵ = r · c   ;    BC ︵ = r · a   e    AC ︵ = r · b

a, b e c sono chiamati angoli centrali dei lati corrispondenti . È consuetudine riferirsi agli angoli centrali al posto dei lati e, in questo caso, il raggio deve essere considerato unità di misura. In questo modo il raggio della sfera non è presente nelle equazioni di trigonometria sferica (in modo simile alla trigonometria piana).

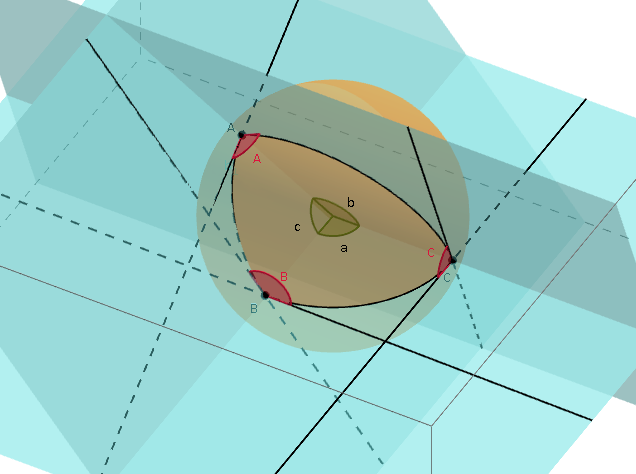
Si possono definire gli angoli interni a un triangolo sferico.

Un angolo di un triangolo sferico è l'angolo tra le rette tangenti ai due lati che si incontrano nel vertice considerato. Gli angoli interni di un triangolo sferico si indicano come i vertici con le lettere romane maiuscole ma in corsivo.

La somma degli angoli interni di un triangolo sferico è sempre più grande di 2π. La differenza è detta eccesso sferico:

E ̂ = A ̂ + B ̂ + C ̂ − π

Quindi, diversamente dai triangoli piani, noti due angoli interni non è possibile conoscere il terzo.

Noto l'eccesso sferico è possibile calcolare l'area del triangolo sferico:

Area = E ̂ · r 2

( E ̂ in radianti).

 2
3

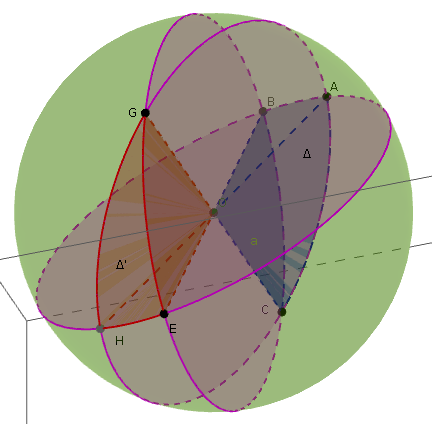
Per dimostrare il teorema dell'eccesso sferico osserviamo la figura in basso a sinistra . Sono disegnati tre circoli massimi. I tre circoli massimi, intersecandosi, formano due triangoli sferici Δ e Δ'. Se consideriamo due circoli massimi, per esempio quello per GE ︵ e quello per GH ︵ , tra i due circoli è compresa una porzione di superficie sferica che dipende dall'angolo G ̂ del triangolo sferico . Si può scrivere la proporzione : S ( G ̂ ) : 4 π r 2 = G ̂ : π . π è l'angolo del triangolo sferico a cui corrisponde l'intera superficie sferica.

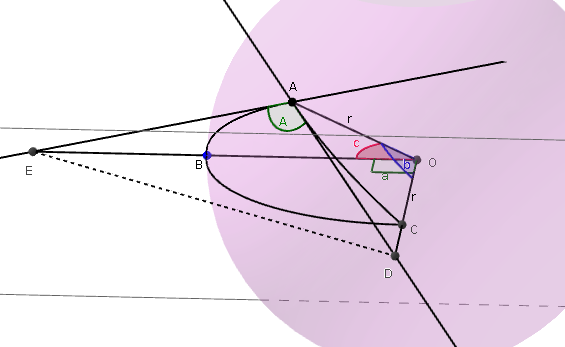
Se per esempio il punto E coincide quasi con A allora G ̂ = π (vedi figura a destra) e l'area della porzione della superficie sferica compresa da una parte e dall'altra di G ̂ è l'intera sfera.

Si ricava : S ( G ̂ ) = 4 r 2 G ̂ . La somma:

S ( A ̂ ) + S ( B ̂ ) + S ( C ̂ ) = 4 r 2 ( A ̂ + B ̂ + C ̂ )

non è uguale all'area della sfera perchè Δ e Δ' sono stati aggiunti sei volte (tre volte Δ e tre volte Δ'). Se vogliamo l'area della sfera bisogna togliere dalla somma 4S(Δ).

Quindi:

S ( A ̂ ) + S ( B ̂ ) + S ( C ̂ ) − 4 S ( Δ ) = 4 π r 2

5
4 Sostituendo la somma degli angoli interni del triangolo sferico:

4 r 2 ( A ̂ + B ̂ + C ̂ ) − 4 S ( Δ ) = 4 π r 2

Ma A ̂ + B ̂ + C ̂ = E ̂ + π ( E ̂ è l'eccesso sferico):

r 2 ( E ̂ + π ) − S ( Δ ) = π r 2 → S ( Δ ) = E ̂ · r 2

Importanti relazioni tra gli angoli interni e angoli centrali sono le tre relazioni di Gauss.

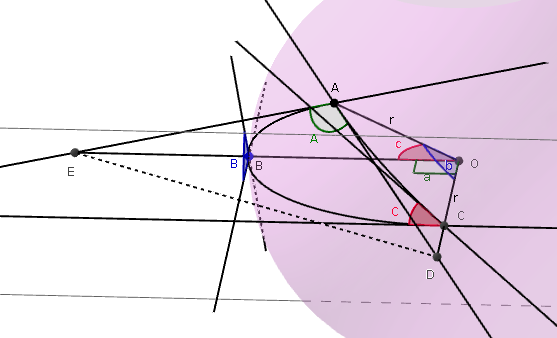
Osservando il triangolo sferico in basso si può applicare il teorema di Carnot ai triangoli ODE e ADE :

DE 2 = OD 2 + OE 2 − 2 · OE · OD · cos a ̂   e   DE 2 = AD 2 + AE 2 − 2 · AD · AE · cos A ̂

Sottraendo la seconda espressione dalla prima :

0 = OD 2 + OE 2 − 2 · OE · OD · cos a ̂ − AD 2 − AE 2 + 2 · AD · AE · cos A ̂

I triangoli OAE e OAD sono rettangoli per costruzione. Da cui, applicando il teorema di Pitagora:

OE 2 = AE 2 + AO 2 = AE 2 + r 2 → OE 2 − AE 2 = r 2

OD 2 = AD 2 + AO 2 = AD 2 + r 2 → OD 2 − AD 2 = r 2

Sostituendo nella precedente espressione:

0 = 2 r 2 − 2 · OE · OD · cos a ̂ + 2 · AD · AE · cos A ̂

Si può osservare dalla figura e dalla definizione di tangente e di coseno di un angolo che si possono scrivere le relazioni:

AD = r · tan b ̂ ; AE = r · tan c ̂ ; OD = r cos b ̂ ; OE = r cos c ̂

Da cui sostituendo nella precedente espressione:

0 = r − r cos c ̂ · r cos b ̂ · cos a ̂ + r · tan b ̂ · r · tan c ̂ · cos A ̂ → 0 = 1 − cos a ̂ cos c ̂ · cos b ̂ + sin b ̂ cos b ̂ · sin c ̂ cos c ̂ · cos A ̂ →

→ cos c ̂ · cos b ̂ = cos a ̂ − sin b ̂ · sin c ̂ · cos A ̂ → cos a ̂ = cos b ̂ · cos c ̂ + sin b ̂ · sin c ̂ · cos A ̂

Prima relazione di Gauss: il coseno di un angolo centrale del triangolo sferico è uguale al prodotto dei coseni degli altri due angoli centrali, più il prodotto dei seni degli stessi angoli centrali per il coseno dell’angolo interno corrispondente.
6
La relazione può essere scritta anche per l'angolo interno B ̂ e centrale b ̂ : cos b ̂ = cos a ̂ · cos c ̂ + sin a ̂ · sin c ̂ · cos B ̂ .

Sostituendo la precedente relazione di Gauss in questa si ha:

cos b ̂ = ( cos b ̂ · cos c ̂ + sin b ̂ · sin c ̂ · cos A ̂ ) · cos c ̂ + sin a ̂ · sin c ̂ · cos B ̂ = cos b ̂ · cos 2 c ̂ + sin b ̂ · sin c ̂ · cos c ̂ · cos A ̂ + sin a ̂ · sin c ̂ · cos B ̂ →

→ cos b ̂ · ( 1 − cos 2 c ̂ ) = sin b ̂ · sin c ̂ · cos c ̂ · cos A ̂ + sin a ̂ · sin c ̂ · cos B ̂ → cos b ̂ · sin 2 c ̂ = sin b ̂ · sin c ̂ · cos c ̂ · cos A ̂ + sin a ̂ · sin c ̂ · cos B ̂ → cos b ̂ · sin c ̂ = sin b ̂ · cos c ̂ · cos A ̂ + sin a ̂ · cos B ̂ →

→ sin a ̂ · cos B ̂ = cos b ̂ · sin c ̂ − sin b ̂ · cos c ̂ · cos A ̂

Seconda relazione di Gauss: il prodotto del seno di un angolo centrale per il coseno di un angolo interno adiacente è uguale al prodotto del coseno dell’angolo centrale corrispondente all'angolo interno adiacente per il seno del terzo angolo centrale meno il prodotto del seno dell'angolo centrale corrispondente l’angolo interno adiacente per il coseno del terzo angolo centrale ed il coseno dell’angolo interno corrispondente al primo angolo centrale.
Dalla prima relazione di Gauss ricaviamo cos A ̂ :

cos A ̂ = cos a ̂ sin b ̂ · sin c ̂ − cos b ̂ · cos c ̂ sin b ̂ · sin c ̂

Elevado al quadrato e sottraendo a 1 si ha:

1 − cos 2 A ̂ = 1 − ( cos a ̂ sin b ̂ · sin c ̂ − cos b ̂ · cos c ̂ sin b ̂ · sin c ̂ ) 2 →

→ sin 2 A ̂ = sin 2 b ̂ · sin 2 c ̂ sin 2 b ̂ · sin 2 c ̂ − ( cos a ̂ sin b ̂ · sin c ̂ − cos b ̂ · cos c ̂ sin b ̂ · sin c ̂ ) 2 →

7

→ sin 2 A ̂ = 1 − cos 2 b ̂ sin 2 b ̂ · sin 2 c ̂ · 1 − cos 2 c ̂ sin 2 b ̂ · sin 2 c ̂ − ( cos a ̂ − cos b ̂ · cos c ̂ ) 2 sin 2 b ̂ · sin 2 c ̂ → sin 2 A ̂ sin 2 a ̂ = 1 − cos 2 c ̂ − cos 2 b ̂ + cos 2 b ̂ · cos 2 c ̂ − cos 2 a ̂ + 2 · cos a ̂ · cos b ̂ · cos c ̂ − cos 2 b ̂ · cos 2 c ̂ sin 2 a ̂ · sin 2 b ̂ · sin 2 c ̂ →

→ sin 2 A ̂ sin 2 a ̂ = 1 − cos 2 a ̂ − cos 2 b ̂ − cos 2 c ̂ + 2 · cos a ̂ · cos b ̂ · cos c ̂ sin 2 a ̂ · sin 2 b ̂ · sin 2 c ̂

L'espessione trovata è simmetrica sia rispetto a ̂ , b ̂ o c ̂ . Si deduce che si può scrivere la relazione:

sin a ̂ sin A ̂ = sin b ̂ sin B ̂ = sin c ̂ sin C ̂

che è la terza relazione di Gauss: il rapporto tra il seno di un angolo centrale del triangolo sferico ed il seno dell’angolo interno corrispondente è costante