LA SFERA CELESTE

LA SFERA CELESTE E LE COORDINATE ASTRONOMICHE


A causa della loro enorme distanza, gli oggetti astronomici ci appaiono proiettati su una sfera ideale concentrica con l’osservatore. Tale sfera prende il nome di sfera celeste e, per definizione, avrà raggio infinito quando l’osservatore è posto al centro di essa, oppure raggio unitario quando si immagina di osservare la sfera dall’esterno. Il centro della sfera celeste è posto sull'osservatore ma, a sua volta, le scelte più frequenti per la posizione dell'osservatore sono : il centro della Terra, il centro del Sole o del baricentro del sistema solare (rispettivamente sfera geocentrica, eliocentrica, baricentrica). Non ci si deve preoccupare della particolare scelta, a meno che la distanza al corpo celeste in esame sia piccola (es. Luna, i pianeti, il Sole, gli asteroidi, le comete, le stelle vicine). Un riferimento utile per le dimensioni angolari degli oggetti sulla sfera celeste sono le dimensioni angolare del Sole e della Luna che sono circa 0.5° (un dito è circa 1°). Nella sfera celeste, poichè le distanze degli oggetti astronomici sono tutte uguali, sono necessarie solo due coordinate per specificare la loro posizione. Qualunque sia la scelta del sistema di coordinate si considera un piano di riferimento passante per il centro della sfera e che divide la sfera in due semisfere secondo un circolo di riferimento. La prima coordinata è la distanza angolare dell'oggetto astronomico da questo circolo di riferimento. Questa distanza angolare è presa su un circolo massimo che passa per il punto ed è perpendicolare al piano di riferimento. La seconda coordinata è la distanza angolare tra l'intersezione del circolo massimo che passa per l'oggetto astronomico e il circolo riferimento con un punto scelto nel circolo di riferimento.
IL SISTEMA ALTAZIMUTALE. Il più naturale sistema di coordinate è il sistema altazimutale o orizzontale . In questo sistema il piano di riferimento è il piano tangente alla superficie terrestre e passante per l'osservatore ed è detto orizzonte astronomico. L'orizzonte astronomico si può definire anche come il piano perpendicolare alla verticale (il piano tangente alla superficie terrestre è il piano perpendicolare alla verticale). Questo piano interseca la sfera celeste in un circolo massimo detto orizzonte. Una retta perpendicolare al piano di riferimento e passante per l'osservatore interserca la sfera celeste in due punti: lo zenit, sopra l'osservatore, e il nadir, sotto l'osservatore. Tutti i circoli massimi passanti per lo zenit e il nadir sono detti circoli verticali. 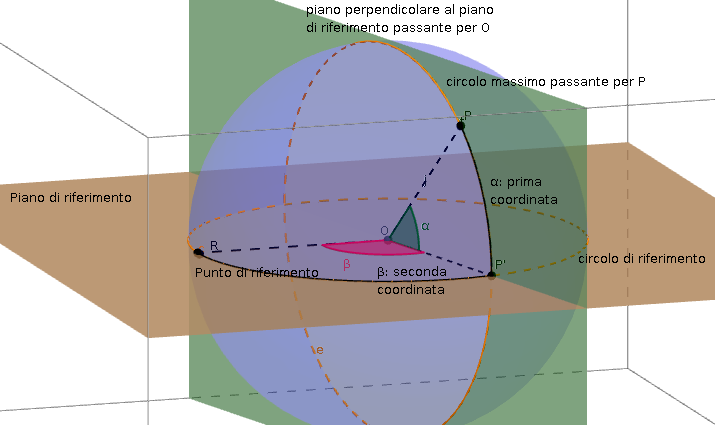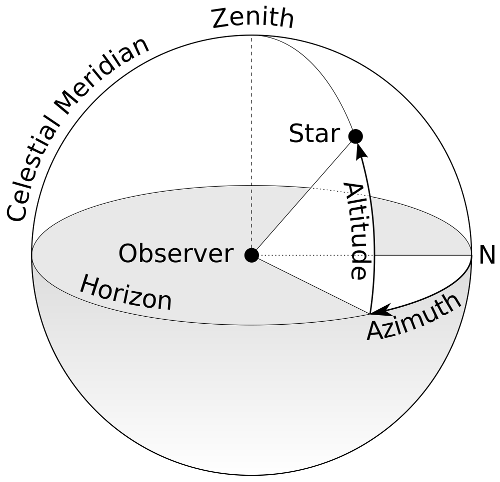Una prima coordinata è la distanza angolare dell'oggetto dall'orizzonte astronomico lungo un circolo verticale. Questa coordinata si chiama altitudine o elevazione (ma è un angolo). L'altitudine è compresa tra +90° e -90°, è positiva per oggetti sopra l'orizzonte e negativa per oggetti sotto l'orizzonte. La distanza zenitale è l'angolo su un circolo massimo tra oggetto e zenith. La distanza zenitale è un angolo complementare all'altitudine. Si osserva che le stelle si muovono nella sfera celeste, sorgono e tramontano, cambiando posizione. Quando raggiungono la più elevata altitudine si dice che sono in culminazione. Tutti i punti di culminazione delle stelle appartengono ad un circolo massimo detto circolo meridiano. Il circolo meridiano interseca l'orizzonte in due punti, il nord geografico e il sud geografico. Se si guarda il nord le stelle sorgono a destra (est) e tramontano a sinistra (ovest). La seconda coordinata è l'azimut, angolo sull'orizzonte a partire da nord o sud (esistono due possibili scelte) in senso orario fino al punto intersezione del circolo verticale che passa sull'oggetto e l'orizzonte. L'azimut è compreso tra 0 e 360°. Le coordinate altazimutali degli oggetti celesti variano nel tempo a causa della rotazione della sfera celeste (rotazione terrestre)
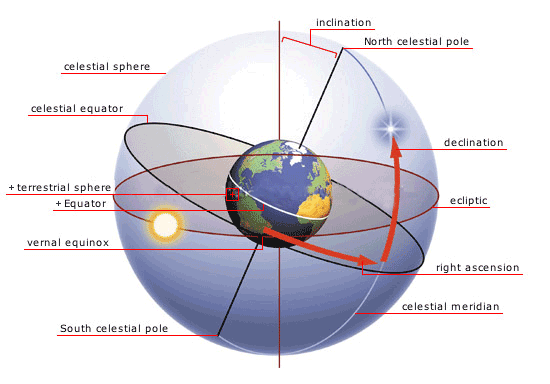
IL SISTEMA EQUATORIALE. In questo sistema il piano di riferimento è il piano equatoriale, piano perpendicolare all'asse di rotazione terrestre. L'intersezione della sfera celeste con piano equatoriale è l'equatore celeste. L'asse di rotazione terrestre interseca la sfera celeste in due punti, il nord celeste e il sud celeste. Tutti i circoli massimi passanti per il polo nord celeste e il polo sud celeste sono detti circoli orari. Il circolo meridiano è un particolare circolo orario che passa anche per il nord geografico e per il sud geogarfico. Il moto apparente delle stelle attorno ai poli avviene secondo circoli minori paralleli all’equatore celeste che prendono il nome di paralleli celesti ( o di declinazione). Nel sistema equatoriale la prima coordinata è la distanza angolare tra oggetto astronomico e l'equatore celeste lungo un circolo orario. Questa coordinata si chima declinazione δ (DEC). La seconda coordinata, quella lungo l'equatore celeste, è presa riferendosi ad un punto particolare detto punto gamma (γ) o punto vernale (punto intersezione tra equatore celeste ed eclittica) e si procede sull'equatore celeste in senso antiorario. Si chiama ascensione retta α (RA) e si misura in ore, minuti e secondi. Un giro completo corrisponde a 24 h. Nel sistema equatoriale l'ascensione retta α e la declinazione δ delle stelle sono fissate in quanto ogni stella sulla sfera celeste si muove su un parallelo celeste (costante declinazione) ma anche il punto γ si muove con la sfera celeste con le stelle (costante ascensione retta). Questa proprietà non vale per il Sole, la Luna, i pianeti, le comete e tutti gli oggetti che definiamo non fissi.
Declinazione e ascensione retta sono indipendenti dalla posizione dell'osservatore (solo se sulla sfera geocentrica) e dal moto della Terra e sono usate per individuare la posizione delle stelle. Tuttavia il punto γ, che è il punto di riferimento per il calcolo delle ascensioni rette, si muove nel tempo e per determinare la posizione di una stella dobbiamo comunque sapere in ogni istante dove è posizionato il punto γ. Allo scopo è stato definito un angolo sull'equatore celeste detto angolo orario h(HA) che è l'angolo, misurato in senso orario, dalla stella al meridiano celeste (il meridiano celeste è fisso) . L'angolo orario del punto γ è detto tempo siderale Θ (ST) . 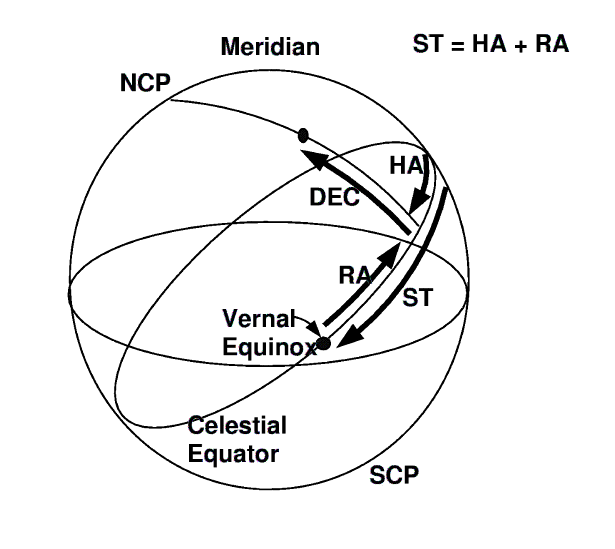Se si conosce il tempo siderale (il tempo siderale si può misurare con l' orologio siderale) e l'ascensione retta di un stella il suo angolo orario sarà : $h = Θ - α$ E, partendo dal meridiano celeste, conoscendo il suo angolo orario, si riesce a trovare la posizione delle stella .
Ma un modo pratico per determinare il tempo siderale è farselo dire da una stella. Si punta il telescopio ad una stella facilmente riconoscibile. Poi si legge l'angolo orario h della stella sulla scala RA del telescopio (se prima si è azzerata la scala puntando il telescopio al polo nord celeste) Si trova dai cataloghi stellari l'ascensione α retta della stella Si ricava il tempo siderale Θ = h + α una volta noto il tempo siderale della stella al momento dell'osservazione si somma il tempo trascorso per calcolare ogni volta il nuovo tempo siderale Se si conosce il tempo siderale Θ si raggiunge il circolo orario di una stella seguendo le fasi: Si trova dai cataloghi stellari l'ascensione retta α della stella Si trova l'angolo oraro h= Θ - α Si ruota il tubo ottico attorno l'asse RA in modo che sulla scala RA compaia l'angolo orario trovato. Per trovare la stella occorre poi ruotare il tubo ottico attorno l'asse DEC in modo da impostare la DEC della stella.