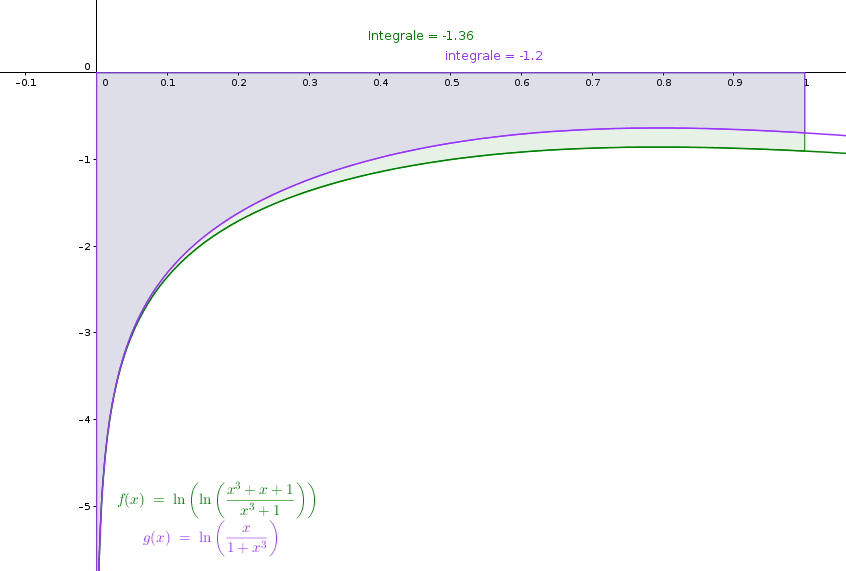
Determinare se il seguente integrale generalizzato è convergente:
La funzione integranda non è continua in x=0.
Per determinare la convergenza consideriamo lo sviluppo di Taylor in x=0 di
, possiamo scrivere:
perchè è infinitesima per x→0.
Se consideramo l'approssimazione al primo termine e lo sostituiamo nella
funzione integranda si ottiene:
Ora proviamo ad integrare per parti l'integrale equivalente:
.
La formula è
La funzione integranda del secondo integrale è definita in x=0.
Inoltre , dove si è fatto uso del limite notevole
. Quindi è convergente e si deduce che anche l'integrale dato è convergente.