
Possiamo dividere l'integrale in due parti:
Per il secondo integrale osserviamo che per x→+∞ e che quindi è infinitesima per x→+∞ di ordine rispetto all'infinitesimo campione allora, per il criterio del confronto asintotico degli integrali generalizzati, è convergente se .
Per il primo integrale consideriamo lo sviluppo di Taylor in x=0 di cos x (fino al terzo termine perchè si può prevedere una semplificazione del secondo termine nel numeratore):
Lo eleviamo al quadrato tenendo i termini fino a x4:
Quindi
Sostituendo nel numeratore equivalente per x→0, l'integrale della funzione equivalente diventa:
Questo limite è finito (=0) solo se è la condizione per la convergenza dell'integrale dato per x→0.
In conclusione l'integrale dato converge se
| Grafici della funzione integranda e della
funzione equivalente x < 1 con α =6.1
|
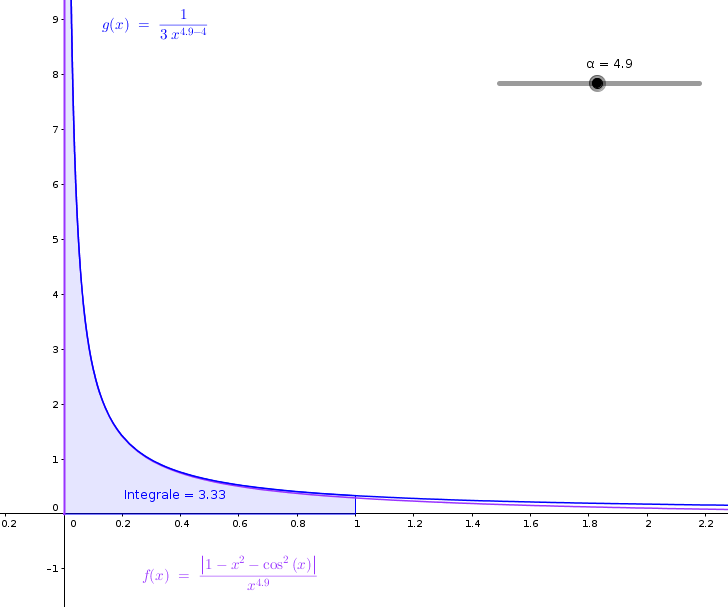
Grafici della funzione integranda e della
funzione equivalente per x<1 con α =4.9
|
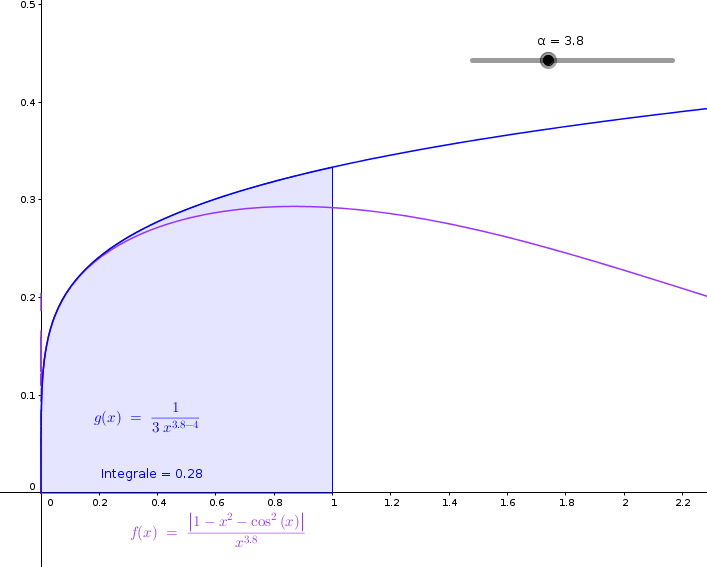
| Grafici della funzione integranda e della
funzione equivalente per x<1 con α =3.8
|
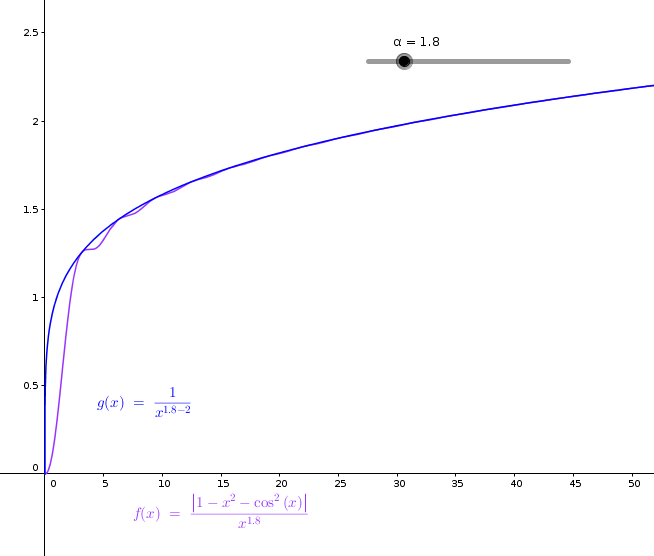
Grafici della funzione integranda e della
funzione equivalente per x>1 con α =1.8
|
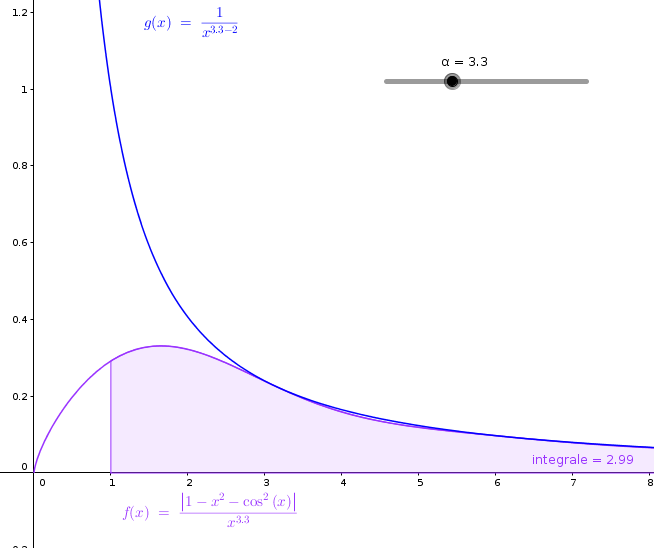
| Grafici della funzione integranda e della
funzione equivalente per x>1 con α =3.3
|
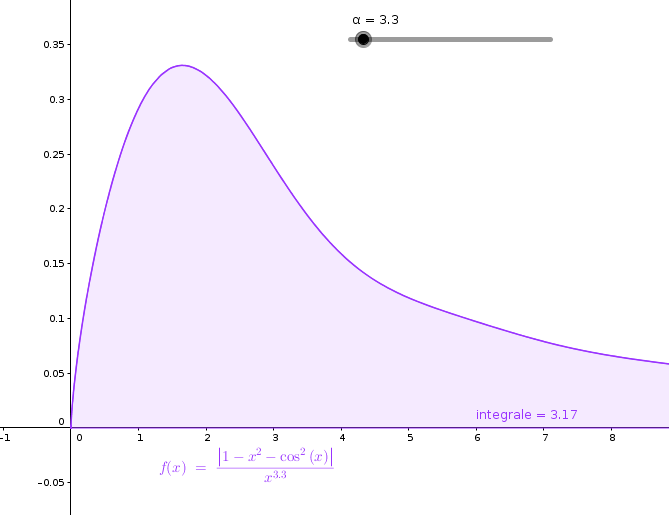
Grafici della funzione integranda e calcolo
dell'integrale dato con α =3.3
|