Data una semicirconferenza di diametro AB= 2r, condurre due corde AC e AD,

la prima uguale al lato del quadrato inscritto, la seconda al lato del triangolo equilatero inscritto nella circonferenza. Determinare:

b. il volume V del solido stesso, applicando i procedimenti di calcolo con integrali definiti dei solidi di rotazione.

Il segmento AD è il lato del triangolo equilatero inscritto in una circonferenza di raggio r: $\overline{\mathrm{AD}}=\sqrt{3}r$

Le coordinate del punto C sono : $C\left(r,r\right)$.

Le coordinate del punto D sono: $D(\frac{3}{2}r,\frac{\sqrt{3}}{2}r)$

Il segmento AC genera un cono di apotema AC e raggio di base r:

$S_1=\mathrm{\pi r}·\overline{\mathrm{AC}}=\mathrm{\pi r}·\sqrt{2}r=\pi \sqrt{2}{r}^2$

Il segmento AD genera un cono di apotema AD e raggio di base $\overline{\mathrm{DH}}=\frac{\sqrt{3}}{2}r$:

$S_2=\pi ·\overline{\mathrm{AD}}·\overline{\mathrm{DH}}=\pi ·\sqrt{3}·\frac{\sqrt{3}}{2}{r}^2=\pi ·\frac{3}{2}{r}^2$

L'arco $\stackrel{︵}{\mathrm{CD}}$genera un segmento sferico a due basi di altezza $h=\overline{\mathrm{AH}}-\overline{\mathrm{AO}}=\frac{3}{2}r-r=\frac{r}{2}$:

$S_3=2\mathrm{\pi r}·h=2\mathrm{\pi r}·\frac{r}{2}=\pi r^2$

L'area della superficie totale del solido generato dalla rotazione del triangolo mistilineo è:

$S=S_1+S_2+S_3=\pi r^2·(\sqrt{2}+\frac{3}{2}+1)=\frac{1}{2}\pi r^2\left(5+2\sqrt{2}\right)$

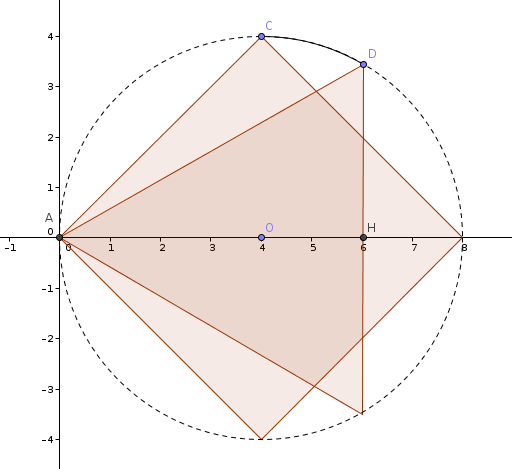
$$L'equazione della retta a cui appartiene il segmento AC è : $y=x$ (bisettrice del primo quadrante).

L'equazione della retta a cui appartiene il segmento AD è: $y=\frac{\sqrt{3}}{3}x$

L'equazione della semicirconferenza data è: $y=\sqrt{2rx-x^2}$

Il volume del solido di rotazione richiesto è dato dall'integrale definito:

$V=\pi ·({\int }_0^{x_C}{x}^2\mathrm{dx}+{\int }_{x_C}^{x_D}\left(2\mathrm{rx}-x^2\right)\mathrm{dx}-{\int }_0^{x_D}\frac{x^2}{3}\mathrm{dx})=\pi ·\left({\int }_0^r{x}^2\mathrm{dx}+{\int }_r^{\frac{3}{2}r}\left(2rx-x^2\right)\mathrm{dx}-\frac{1}{3}{\int }_0^{\frac{3}{2}r}{x}^2\mathrm{dx}\right)=\pi ·[\frac{r^3}{3}+r·(\frac{9}{4}{r}^2-r^2)-\frac{1}{3}·(\frac{27}{8}{r}^3-r^3)-\frac{1}{9}·\frac{27}{8}{r}^3]=$

$=\pi r^3·(\frac{1}{3}+\frac{5}{4}-\frac{19}{24}-\frac{3}{8})=\pi r^3·\frac{8+30-19-9}{24}=\frac{5}{12}\pi r^2$