Problemi con le funzioni N° 10

Prima di individuare i due intervalli occorre conoscere qualcosa di più sulla funzione.

Il campo di esistenza. CE= R
Intercetta f(0)= -14
Asintoti.

Orizzontale.

$\underset{x \to + \infty}{l i m} e^{2 x} - 2 x - 15 = \underset{x \to + \infty}{l i m} e^{2 x} (1 - \frac{2 x + 15}{e^{2 x}}) = \underset{x \to + \infty}{l i m} e^{2 x} \cdot \underset{x \to + \infty}{l i m} (1 - \frac{2 x + 15}{e^{2 x}}) = \underset{x \to + \infty}{l i m} e^{2 x} \cdot (\underset{x \to + \infty}{l i m} 1 - \underset{x \to + \infty}{l i m} \frac{2 x + 15}{e^{2 x}}) =$

$= \underset{x \to + \infty}{l i m} e^{2 x} \cdot (1 - \underset{x \to + \infty}{l i m} \frac{25}{{2 e}^{2 x}}) = \underset{x \to + \infty}{l i m} e^{2 x} \cdot (1 - 0) = + \infty$

$\underset{x \to - \infty}{l i m} e^{2 x} - 2 x - 15 = + \infty$

Non esistono asintoti orizzontali.

Obliqui. $f' (x) = 2 e^{2 x} - 2.$ ${\begin{matrix} \underset{x \to + \infty}{l i m} & 2 e^{2 x} - 2 = + \infty \\ \underset{x \to - \infty}{l i m} & 2 e^{2 x} - 2 = - 2 \end{matrix}$

Un asintoto obliquo.

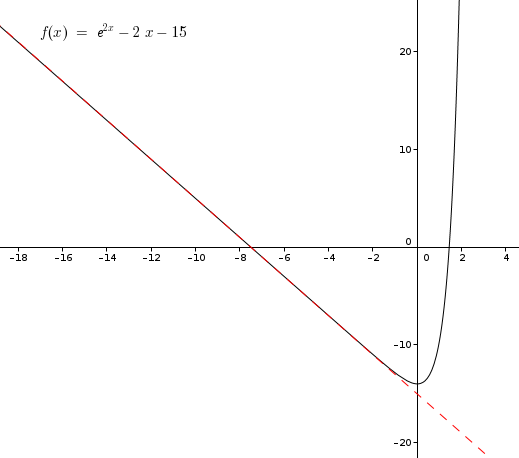
$q = \underset{x \to - \infty}{l i m} (f (x) - f' (x) \cdot x) = \underset{x \to - \infty}{l i m} [e^{2 x} - 2 x - 15 - (2 e^{2 x} - 2) \cdot x] = \underset{x \to - \infty}{l i m} [e^{2 x} - 2 x - 15 - 2 x e^{2 x} + 2 x] = \underset{x \to - \infty}{l i m} [{(1 - 2 x) e}^{2 x} - 15] =$

= \underset{x \to - \infty}{l i m} [\frac{(1 - 2 x)}{e^{- 2 x}} - 15] = \underset{x \to - \infty}{l i m} \frac{(1 - 2 x)}{e^{- 2 x}} - \underset{x \to - \infty}{l i m} 15 = \underset{x \to - \infty}{l i m} \frac{- 2}{- 2 \cdot e^{- 2 x}} - \underset{x \to - \infty}{l i m} 15 = \underset{x \to - \infty}{l i m} \frac{1}{e^{- 2 x}} - \underset{x \to - \infty}{l i m} 15 = \underset{x \to - \infty}{l i m} e^{2 x} - \underset{x \to - \infty}{l i m} 15 = - 15

L'asintoto obliquo ha equazione y= -2x - 15

È evidente, dallo studio degli asintoti e dalla conoscenza dell'intercetta, che la funzione deve avere almeno due radici.

Estremi. $f' (x) = 2 e^{2 x} - 2.$ Posta f'(x)= 0 si ricava: x=0. Nell'intercetta c'è un estremo e poiché f'(x) >0 per x> 0 l'estremo deve essere un minimo.

Da queste considerazioni si deduce che esistono solo due radici.

Concavità. $f " (x) = 4 e^{2 x}$ . La derivata seconda è sempre positiva, la concavità della funzione è sempre rivolta verso l'alto.

Applicando il metodo delle separazione delle variabili si ottiene:

{\begin{matrix} y = e^{2 x} \\ y = 2 x + 15 \end{matrix}

. Posto 2x+15=0 si ha: x= -15/2 . In un intorno di questo punto come [-8; -7] deve esistere la radice di minor valore. In x= -8 f(-8) ≃ 1.0000001125 > 0, in x= -7, f(-7)= -0.999999165 <0 . Quindi un primo intervallo in cui è verificato il teorema di esistenza degli zeri è [-8 ; -7]. Un secondo intervallo potrebbe essere [0; +∞[ ma, dato che la derivata seconda è positiva, per questo secondo intervallo occorre far partire le tangenti dall'estremo destro che non può essere non definito. Per trovare un estremo destro in cui la funzione è positiva, dato che la funzione e^2x cresce rapidamente, si può provare f(1)= e² - 2 - 15 ≃ -9.6 ; f(2)= e⁴- 8 - 15 ≃ 32 > 0 . Così, un intervallo dove si trova la radice di maggior valore è [0; 2].

b	$c = b - \frac{f (b)}{f' (b)} = b - \frac{b^{2} - l n (b) - 15}{\frac{2 b^{2} - 1}{b}} = \frac{2 b^{3} - b - b^{3} + b \cdot l n (b) + 15 b}{2 b^{2} - 1} = b \cdot [\frac{b^{2} + l n (b) + 14}{2 b^{2} - 1}]$	$f (b) = b^{2} - l n (b) - 15$	\|c-b\|
2	1.6679162433	35.5981500331	0.3320837567
1.6679162433	1.4877446876	9.7659353459	0.1801715557
1.4877446876	1.444094374	1.6237228949	0.0436503136
1.444094374	1.4419553195	0.0725599327	0.0021390545

Per quanto riguarda la radice di minor valore, dato che f(-8) >0, occorre considerare l'estremo sinistro dell'intervallo [-8, -7] da cui far partire le tangenti.

a	$c = a - \frac{f (a)}{f' (a)} = a - \frac{a^{2} - l n (a) - 15}{\frac{2 a^{2} - 1}{a}} = \frac{2 a^{3} - a - a^{3} + a \cdot l n (a) + 15 a}{2 a^{2} - 1} = a \cdot [\frac{a^{2} + l n (a) + 14}{2 a^{2} - 1}]$	$f (a) = a^{2} - l n (a) - 15$	\|c-a\|
-8	-7.4999998875	1.0000001125	0.5000001125
-7.4999998875	-7.499999847	8.08320148593111E-008	4.04160198641534E-008

Si raggiunge molto presto l'approssimazione asintotica della f(x) ad una retta quando x tende a meno infinito.

Occorre infine calcolare il volume del solido di rotazione richiesto.

$V = π \int_{- 7.5}^{1.44} {(e^{2 x} - 2 x - 15)}^{2} ⅆ x$

$\int {(e^{2 x} - 2 x - 15)}^{2} ⅆ x = \int e^{4 x} ⅆ x + 4 \int x^{2} ⅆ x + 225 \int ⅆ x - 4 \int x e^{2 x} ⅆ x - 30 \int e^{2 x} ⅆ x + 60 \int x ⅆ x$

$\int x e^{2 x} ⅆ x . {\begin{matrix} F (x) = x & g (x) = e^{2 x} \\ f (x) = 1 & G (x) = \frac{e^{2 x}}{2} \end{matrix} \to \int x e^{2 x} ⅆ x = \frac{x e^{2 x}}{2} - \frac{1}{2} \int e^{2 x} ⅆ x = \frac{x e^{2 x}}{2} - \frac{e^{2 x}}{4}$

$\int {(e^{2 x} - 2 x - 15)}^{2} ⅆ x = \frac{e^{4 x}}{4} + \frac{4}{3} \cdot x^{3} + 225 x - 2 x e^{2 x} + e^{2 x} - 30 \frac{e^{2 x}}{2} + 30 x^{2} = \frac{e^{4 x}}{4} - 2 x e^{2 x} - 14 e^{2 x} + \frac{4}{3} \cdot x^{3} + 30 x^{2} + 225 x$

$V = π \int_{- 7.5}^{1.44} {(e^{2 x} - 2 x - 15)}^{2} ⅆ x = π \cdot {[\frac{e^{4 x}}{4} - 2 x e^{2 x} - 14 e^{2 x} + \frac{4}{3} \cdot x^{3} + 30 x^{2} + 225 x]}_{- 7.5}^{1.44} =$

= π \cdot [(\frac{e^{4 \cdot (1.44)}}{4} - 2 \cdot (1.44) e^{2 \cdot (1.44)} - 14 e^{2 \cdot (1.44)} + \frac{4}{3} \cdot {(1.44)}^{3} + 30 \cdot {(1.44)}^{2} + 225 \cdot (1.44)) - (\frac{e^{4 \cdot (- 7.5)}}{4} - 2 \cdot (- 7.5) e^{2 \cdot (- 7.5)} - 14 e^{2 \cdot (- 7.5)} + \frac{4}{3} \cdot {(- 7.5)}^{3} + 30 \cdot {(- 7.5)}^{2} + 225 \cdot (- 7.5))] =

≃ π [168.82 - (- 562.5)] = π 731.32 ≃ 2297.5