È facile osservare che  d dx [ ln( 2- x 2 + x 3 ) ]= 3 x 2 -2x 2- x 2 + x 3   e che il calcolo dell'integrale  ∫ 3 x 2 -2x 2- x 2 + x 3 ⋅ ln( 2- x 2 + x 3 ) ⁢ ⅆ x  si opera immediatamente con l'applicazione della formula: ∫ [f⁡(x)] n ⋅ f'⁡(x) ⁢ ⅆ x = [f⁡(x)] n+1 n+1 +c  con n=1. 
Quindi le primitive cercate si scrivono: F⁡(x)= ∫ 3 x 2 -2x 2- x 2 + x 3 ⋅ ln( 2- x 2 + x 3 ) ⁢ ⅆ x = 1 2 ⋅ l n 2 ( 2- x 2 + x 3 )+c .
La primitiva che passa per A( 2; 1 2 l n 2 6 ) si individua sostituendo l'ascissa e l'ordinata nella generica primitiva:

1 2 ⋅ l n 2 6= 1 2 ⋅ l n 2 ( 2- (2) 2 + (2) 3 )+c → c= 1 2 ⋅ l n 2 6- 1 2 ⋅ l n 2 ( 2-4+8 )= 1 2 ⋅ l n 2 6- 1 2 ⋅ l n 2 (6)=0

Con c=0 è:  F⁡(x)= 1 2 ⋅ l n 2 ( 2- x 2 + x 3 )


Lo studio di F(x).
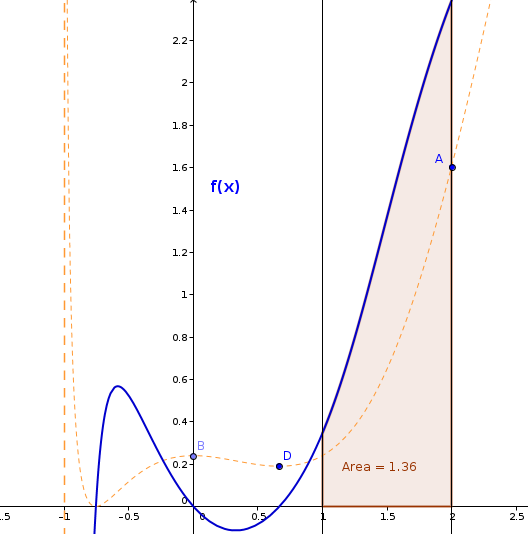
  1. Campo di esistenza.  Occorre imporre 2- x 2 + x 3 >0 . Si può osservare che in questa disequazione di terzo grado una radice è x= -1. Applicando la regola di Ruffini la disequazione diventa: ( x+1 ) ⋅ ( x 2 -2x+2 )>0 . La disequazione di secondo grado non ha soluzioni reali. Quindi per il campo di esistenza bisogna imporre solo la condizione : x > -1.
  2. Radici e intercetta. Per le radici occorre imporre: 2- x 2 + x 3 =1 → x 3 - x 2 +1=0  . Questa equazione cubica che può essere risolta con metodi numerici.
Scritta q(x)= x³ - x² +1 si può osservare che q(-1)= -1 e q(0)= 1. Allora la radice deve trovarsi nell'intervallo [-1;0]. Inoltre si ha che q"(x)= 6x - 2 e che q"(x)>0 se x> 1/3, quindi nell'intervallo considerato q"(x) mantiene lo stesso segno ed è minore di zero (concavità verso il basso). È applicabile il metodo delle tangenti o delle secanti. Il metodo delle tangenti è veloce se è facile trovare la derivata prima. Come in questo caso.

q(0)·q"(x)<0
a

 c=a- q⁡(a) q'⁡(a) =a- a 3 - a 2 +1 3 a 2 -2a = 3 a 3 -2 a 2 - a 3 + a 2 -1 3 a 2 -2a = 2 a 3 - a 2 -1 3 a 2 -2a
-1
 c= 2 ( -1 ) 3 - ( -1 ) 2 -1 3 ( -1 ) 2 -2( -1 ) =- 4 5
-4/5
 c= 2 ( - 4 5 ) 3 - ( - 4 5 ) 2 -1 3 ( - 4 5 ) 2 -2( - 4 5 ) = - 128 125 - 16 25 -1 48 25 + 8 5 = -128-80-125 240+200 =- 333 440 ≃ -0.757

  ε= |-4/5 - (-333/440)|= |-19/440| ≃ 0.043.  Trovare l'intercetta invece è semplice: F⁡(0)= 1 2 ⋅ l n 2 (2) ≃ 0.24 
  1. Segno della funzione. Data la presenza di un quadrato la funzione è positiva in tutto il suo campo di esistenza. Da questa considerazione si deduce che la radice della funzione è tale che l'asse della ascisse è tangente nel punto di radice e non secante.
  2. Asintoti. Un asintoto verticale in x= -1: lim x → - 1 + 1 2 ⋅ l n 2 ( 2- x 2 + x 3 )=+ ∞ . Inoltre lim x → + ∞ 1 2 ⋅ l n 2 ( 2- x 2 + x 3 )=+ ∞
  3. Punti estremi. F'⁡(x)=f⁡(x)= 3 x 2 -2x 2- x 2 + x 3 ⋅ ln( 2- x 2 + x 3 ) . Un estremo (C) si trova imponendo la condizione:  2- x 2 + x 3 =1 → x 3 - x 2 +1=0 ;   l'estremo allora coincide con la radice ed è un minimo assoluto essendo la funzione sempre positiva .
Altri estremi si trovano imponendo la condizione: 3 x 2 -2x=0 → x B =0 ∧ x D = 2 3 . 
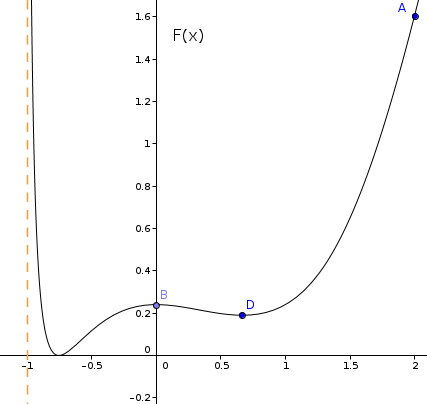
Da cui anche le ordinate:  y B = 1 2 ⋅ l n 2 (2)  e y D = 1 2 ⋅ l n 2 ( 2- ( 2 3 ) 2 + ( 2 3 ) 3 )= 1 2 ⋅ l n 2 ( 2- 4 9 + 8 27 )= 1 2 ⋅ l n 2 ( 54-12+8 27 )= 1 2 ⋅ l n 2 ( 50 27 ) ≃ 0.19
Per la sua complessità qui si chiude lo studio della funzione F(x). 
L'area della regione finita di piano compresa tra le rette di equazioni x=1, x=2, l'asse delle ascisse e il grafico della funzione f(x) è data dal calcolo dell'integrale definito:
A= ∫ 1 2 3 x 2 -2x 2- x 2 + x 3 ⋅ ln( 2- x 2 + x 3 ) ⁢ ⅆ x = [F⁡(x)] 1 2 =[ 1 2 ⋅ l n 2 ( 2- 2 2 + 2 3 )- 1 2 ⋅ l n 2 ( 2- 1 2 + 1 3 ) ]= 1 2 ⋅ ( l n 2 6-l n 2 2 )