Problemi con funzioni N° 8

Prima condizione. k₁ e k₂ passano per l'origine. Deve essere c= 0.
Seconda condizione. k₁ e k₂ passano per il punto A(2; 0). Sostituendo si ottiene:

0 = 8 + 4 a + 2 b \to 2 a + b = - 4

Terza condizione. k₁ e k₂ sono tangenti all'asse delle ascisse. Occorre calcolare la derivata prima: y'= 3x² + 2ax + b , e porla uguale a zero, sostituendo poi alle x e y le coordinate dei punti di tangenza. Sostituendo si ottiene:

{\begin{matrix} k_{2} : & 0 = 12 + 4 a + b \to {\begin{matrix} 4 a + b = - 12 \\ 2 a + b = - 4 \end{matrix} \to {\begin{matrix} 2 a = - 8 \to a = - 4 \\ b = - 4 - 2 a \end{matrix} \to {\begin{matrix} a = - 4 \\ b = 4 \end{matrix} \to k_{2} : y = x^{3} - 4 x^{2} + 4 x \\ k_{1} : & 0 = b \to {\begin{matrix} 2 a + b = - 4 \\ b = 0 \end{matrix} \to {\begin{matrix} a = - 2 \\ b = 0 \end{matrix} \to k_{1} : y = x^{3} - 2 x^{2} \end{matrix}

Andamento di k₁ e k₂.

k₁ : f(x)= x³ - 2x²

Dominio di definizione. C.E.= R
Simmetrie. f(x-)= -x³+2x² ≠ f(x) ⋀ ≠ -f(x). Nessuna simmetria rispetto gli assi cartesiani
Radici e intercetta. Intercetta è l'origine degli assi. Le radici in x=0 e in x= 2 (intercetta coincidente con una radice).
Asintoti

Orizzontale. $\underset{x \to + \infty}{l i m} x^{3} - 2 x^{2} = + \infty$ e $\underset{x \to - \infty}{l i m} x^{3} - 2 x^{2} = - \infty$
Obliquo. Dall'esame dell'asintoto orizzontale si evince che anche gli obliqui non esistono per f(x)

Segno della funzione. Posto f(x)=x²·(x-2) si vede che f(x) ≥ 0 ∀x ∈ [2, +∞[.
Estremi. f'(x)= 3x² - 4x . Posto f'(x)=0 si ottiene x=0 e x= 4/3. Quindi due punti estremi; uno coincidente con la radice e l'origine e il secondo in x= 4/3 e ordinata y= -32/27.
Segno della derivata prima. f'(x) ≥ 0 → 3x² - 4x ≥ 0 → x ∈ ]-∞; 0] ∪ [4/3; +∞[ . Si deduce che in x=0 c'è un massimo relativo e in x= 4/3 un minimo relativo.
Derivata seconda. f"(x)= 6x - 4. Un flesso in x= 2/3. Ordinata del flesso y= -16/27

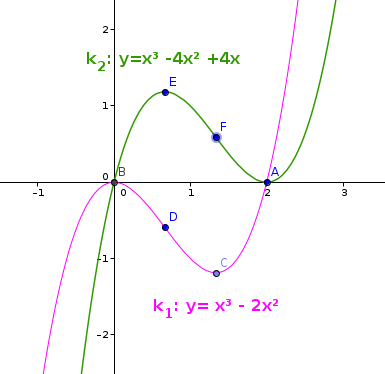
k₂: f(x)= x³ - ^4x² + 4x

Dominio di definizione. C.E.= R
Simmetrie. f(x-)= -x³ -4x² - 4x ≠ f(x) ⋀ ≠ -f(x). Nessuna simmetria rispetto gli assi cartesiani
Radici e intercetta. Intercetta è l'origine degli assi. Le radici in x=0 e nella soluzione della disequazione x² - 4x + 4=0 → x=2
Asintoti

Orizzontale. $\underset{x \to + \infty}{l i m} x^{3} - 4 x^{2} + 4 x = + \infty$ e $\underset{x \to - \infty}{l i m} x^{3} - 4 x^{2} + 4 x = - \infty$
Obliquo. Dall'esame dell'asintoto orizzontale si evince che anche gli obliqui non esistono per f(x)

Segno della funzione. Posto f(x)=x·(x-2)² si vede che f(x) ≥ 0 ∀x ∈ [0, +∞[.
Estremi. f'(x)= 3x² - 8x + 4 . Posto f'(x)=0 si ottiene x=2 e x= 2/3. Quindi due punti estremi; uno coincidente con la radice e il secondo in x= 2/3 e ordinata y= 32/27.
Segno della derivata prima. f'(x) ≥ 0 → 3x² - 8x + 4 ≥ 0 → x ∈ ]-∞; 2/3] ∪ [2; +∞[ . Si deduce che in x=2/3 c'è un massimo relativo e in x= 2 un minimo relativo.
Derivata seconda. f"(x)= 6x - 8. Un flesso in x= 4/3. Ordinata del flesso y= 16/27

Calcolo dell'area S₁.

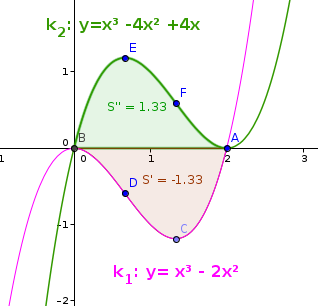
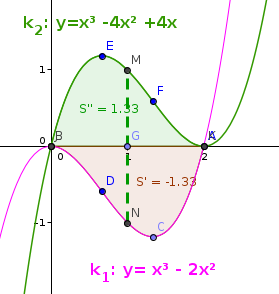
$S_{1} = \int_{0}^{2} (x^{3} - 4 x^{2} + 4 x) ⅆ x + | \int_{0}^{2} x^{3} - 2 x^{2} ⅆ x | = \int_{0}^{2} (x^{3} - 4 x^{2} + 4 x) ⅆ x - \int_{0}^{2} (x^{3} - 2 x^{2}) ⅆ x = \int_{0}^{2} (x^{3} - 4 x^{2} + 4 x - x^{3} + 2 x^{2}) ⅆ x =$

$= \int_{0}^{2} (- 2 x^{2} + 4 x) ⅆ x = 2 {[- \frac{x^{3}}{3} + 2 \cdot \frac{x^{2}}{2}]}_{0}^{2} = 2 (- \frac{8}{3} + 4) = \frac{8}{3}$

Bisogna imporre che la distanza fra un punto di k₂e un punto dik₁, di uguale ascissa,sia massima. Ovvero che la differenza tra l'ordinata di k₂ e quella di k₁sia massima: $D = y_{2} - y_{1} = x^{3} - 4 x^{2} + 4 x - x^{3} + 2 x^{2} = - 2 x^{2} + 4 x .$

Derivando: $\frac{d D}{d x} = - 4 x + 4 = 0 \to x = 1; D = 2$ . Corda di ascissa 1 e lunghezza 2

La trasformazione S: ${\begin{matrix} x = 2 - x' \\ y = -y' \end{matrix}$ è una simmetria centrale di centro C(1; 0).

Applicata alla k₂ si ottiene:
$S \cdot k_{2} = k_{2}^{'} \to {\begin{matrix} x = 2 - x' \\ y = -y' \end{matrix} \to$ $- y' = (2 - x')^{3} - 4 (2 - x')^{2} + 4 (2 - x') \to$
$- y' = 8 + 6 x'^{2} - 12 x' - x'^{3} - 16 - 4 x'^{2} + 16 x' + 8 - 4 x' = - x'^{3} + 2 x'^{2} \to y' = x'^{3} - 2 x'^{2} (k_{1})$

Applicata alla k₁ si ottiene:
$S \cdot k_{1} = k_{1}^{'} \to {\begin{matrix} x = 2 - x' \\ y = -y' \end{matrix} \to$ $- y' = (2 - x')^{3} - 2 (2 - x')^{2} =$
$- y' = 8 + 6 x'^{2} - 12 x' - x'^{3} - 8 - 2 x'^{2} + 8 x' = - x'^{3} + 4 x'^{2} - 4 x' \to y' = x'^{3} - 4 x'^{2} + 4 x' (k_{2})$

La retta y= 1/2 interseca, nella regione R, la curva k₂: 1/2 = x³ -4x² + 4x → 2x³ - 8x² + 8x - 1= 0. Per risolvere questa equazione, che nella regione R avrà due radici, occorre trovare due intervalli in cui la funzione h(x) = 2x³ - 8x² + 8x - 1 soddisfa il teorema di esistenza degli zeri. Si può applicare il metodo di separazione delle radici, ma avendo studiato la curva k₂è immediato osservare che sicuramente y < 1/2 per x=0 e x> 1/2 per x= x_E (massimo relativo). Quindi un primo intervallo è [0; 2/3]. Il secondo intervallo è sicuramente [2/3, 2] (sia in x=0, che in x=2 la funzione si annulla). Si può applicare il metodo delle tangenti perché h"(x)= 12x - 16 > 0 → ∀ x > 4/3 la derivata seconda è positiva.

Intervallo [0; 2/3] . h"(x) < 0 e h(2/3) > 0. L'estremo da cui partiranno le tangenti è quello sinistro.

a
$c = a - \frac{h (a)}{h' (a)} = a - \frac{2 a^{3} - 8 a^{2} + 8 a - 1}{6 a^{2} - 16 a + 8} = \frac{6 a^{3} - 16 a^{2} + 8 a - 2 a^{3} + 8 a^{2} - 8 a + 1}{6 a^{2} - 16 a + 8} = \frac{4 a^{3} - 8 a^{2} + 1}{6 a^{2} - 16 a + 8}$
$h (c) = 2 c^{3} - 8 c^{2} + 8 c - 1$
|c-a|

0     0.125
-0.12109375   0.125

0.125          0.1448717949
-0.0028472454 0.0198717949

0.1448717949 0.1453620249
-1.71346995392341E-6
0.00049023

0.1453620249     0.1453623203
-6.21724893790088E-13
2.95375522596508E-7