Problemi con le funzioni N° 9

Prima di individuare i due intervalli occorre conoscere qualcosa di più sulla funzione.

Il campo di esistenza. CE= R⁺
Asintoti.

Orizzontale.

$\underset{x \to + \infty}{l i m} x^{2} - l n (x) - 15 = \underset{x \to + \infty}{l i m} x^{2} \cdot (1 - \frac{l n (x) + 15}{x^{2}}) = \underset{x \to + \infty}{l i m} x^{2} \cdot \underset{x \to + \infty}{l i m} (1 - \frac{l n (x) + 15}{x^{2}}) = \underset{x \to + \infty}{l i m} x^{2} \cdot (\underset{x \to + \infty}{l i m} 1 - \underset{x \to + \infty}{l i m} \frac{l n (x) + 15}{x^{2}}) =$

$= \underset{x \to + \infty}{l i m} x^{2} \cdot (\underset{x \to + \infty}{l i m} 1 - \underset{x \to + \infty}{l i m} \frac{\frac{1}{x}}{2 x}) = \underset{x \to + \infty}{l i m} x^{2} \cdot (\underset{x \to + \infty}{l i m} 1 - \underset{x \to + \infty}{l i m} \frac{1}{2 x^{2}}) = \underset{x \to + \infty}{l i m} x^{2} \cdot (\underset{x \to + \infty}{l i m} 1 - 0) = \underset{x \to + \infty}{l i m} x^{2} \cdot (1) = + \infty$

Non esistono asintoti orizzontali.

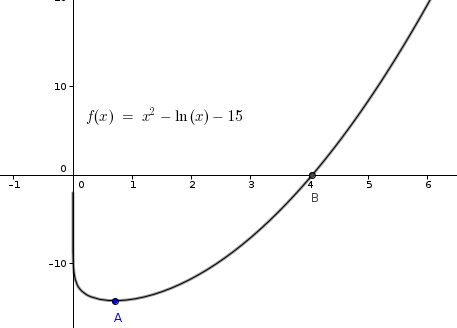
Verticale. Nel punto di discontinuità: $\underset{x \to 0^{+}}{l i m} x^{2} - l n (x) - 15 = + \infty$

È evidente, dallo studio degli asintoti, che la funzione, continua in R⁺, o ha due radici o non ha nessuna radice.

Estremi. $f' (x) = 2 x - \frac{1}{x} = \frac{2 x^{2} - 1}{x}$ . Posta f'(x)= 0 si ricava: x=√2/2 nel CE della funzione.

Inoltre: $f (\frac{1}{\sqrt{2}}) = \frac{1}{2} - l n (2^{- \frac{1}{2}}) - = \frac{1}{2} [1 + l n (2)] - 15 <

0.$ Quindi un minimo è collocato nel quarto quadrante. Questo significa che esistono due radici.

Concavità. $f'' (x) = \frac{d}{d x} (2 x - \frac{1}{x}) = 2 + \frac{1}{x^{2}}$ . La derivata seconda è sempre positiva, la concavità della funzione è sempre rivolta verso l'alto.

Applicando il metodo delle separazione delle variabili si ottiene:

{\begin{matrix} y = x^{2} \\ y = l n (x) + 15 \end{matrix}

. Posto ln(x) + 15=0 si ha: ln(x)= -15 → x= e^-15. In questo punto f(x) è sicuramente positiva. In x= 1 f(1) = 1 - 15 < 0 . Quindi un primo intervallo in cui è verificato il teorema di esistenza degli zeri è [ e^-15; 1]. Un secondo intervallo potrebbe essere [1; +∞[ ma, dato che la derivata seconda è positiva, per questo secondo intervallo occorre far partire le tangenti dall'estremo destro che non può essere non definito. Per trovare un estremo destro in cui la funzione è positiva si può considerare che dopo un certo x, x² - ln(x) ≃ x², da cui ponendo x²= 15 si ricava che l'altro estremo deve essere poco maggiore di √15. Infatti per esempio: (√15+1)² - ln(√15+1) - 15 = 1 + 2√15 - ln(√15+1) ≃ 7.16 > 0

b	$c = b - \frac{f (b)}{f' (b)} = b - \frac{b^{2} - l n (b) - 15}{\frac{2 b^{2} - 1}{b}} = \frac{2 b^{3} - b - b^{3} + b \cdot l n (b) + 15 b}{2 b^{2} - 1} = b \cdot [\frac{b^{2} + l n (b) + 14}{2 b^{2} - 1}]$	$f (b) = b^{2} - l n (b) - 15$	\|c-b\|
√15+1	4.1222816041	7.1622603461	0.7507017421
4.1222816041	4.0501995831	0.5767988257	0.072082021
4.0501995831	4.0495182939	0.0053505029	0.0006812892

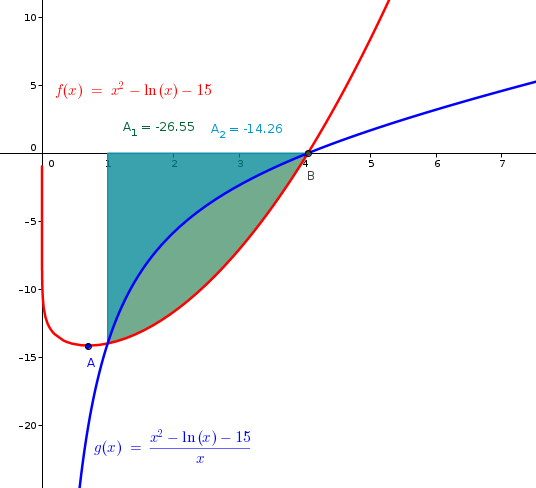
Per calcolare l'area di piano compresa fra f(x) e g(x)= f(x)/x occorre conoscere i loro punti di intersezione:

f (x) = \frac{f (x)}{x} \to f (x) - \frac{f (x)}{x} = 0 \to \frac{x - 1}{x} \cdot f (x) = 0

Un punto di intersezione è x=1 e altri due punti dall'equazione f(x)=0. Poiché è stato richiesto solo il calcolo della radice di maggior valore di f(x) si deduce che l'area di piano è quella compresa tra i punti x= 1 e x≃ 4.05.
Consideriamo ora le due aree e osserviamo i segni.

$A_{1} = \int_{1}^{4.05} f (x) ⅆ x = \int_{1}^{4.05} (x^{2} - l n (x) - 15) ⅆ x$

$\int x^{2} ⅆ x = \frac{x^{3}}{3}$
$\int l n (x) ⅆ x . {\begin{matrix} F (x) = l n (x) & g (x) = 1 \\ f (x) = \frac{1}{x} & G (x) = x \end{matrix} \to$ $\int l n (x) ⅆ x = x \cdot l n (x) - \int ⅆ x = x \cdot l n (x) - x = (x - 1) \cdot l n (x)$
$\int 15 ⅆ x = 15 x$

$A_{1} = {[\frac{x^{3}}{3} - (x - 1) \cdot l n (x) - 15 x]}_{1}^{4.05} = (\frac{4.0 5^{3}}{3} - (4.05 - 1) \cdot l n (4.05) - 15 \cdot 4.05) - (\frac{1^{3}}{3} - (1 - 1) \cdot l n (1) - 15 \cdot 1) ≃ - 26.55$

$A_{2} = \int_{1}^{4.05} \frac{f (x}{x}) ⅆ x = \int_{1}^{4.05} (\frac{x^{2} - l n (x) - 15}{x}) ⅆ x = \int_{1}^{4.05} (x - \frac{l n (x)}{x} - \frac{15}{x}) ⅆ x$

$\int x ⅆ x = \frac{x^{2}}{2}$
$\int \frac{l n (x)}{x} ⅆ x . {\begin{matrix} F (x) = l n (x) & g (x) = \frac{1}{x} \\ f (x) = \frac{1}{x} & G (x) = l n (x) \end{matrix} \to$ $\int \frac{l n (x)}{x} ⅆ x = l n^{2} (x) - \int \frac{l n (x)}{x} ⅆ x \to \int \frac{l n (x)}{x} ⅆ x = \frac{1}{2} \cdot l n^{2} (x)$
$\int \frac{15}{x} ⅆ x = 15 \cdot l n (x)$

$A_{2} = {[\frac{x^{2}}{2} - \frac{1}{2} \cdot l n^{2} (x) - 15 \cdot l n (x)]}_{1}^{4.05} = (\frac{4.0 5^{2}}{2} - \frac{1}{2} \cdot l n^{2} (4.05) - 15 \cdot l n (4.05)) - (\frac{1^{2}}{2} - \frac{1}{2} \cdot l n^{2} (1) - 15 \cdot l n (1)) ≃ - 14.25$

L'area cercata allora sarà A= |A₂ - A₁| ≃ 14

L'intervallo che contiene la radice di minor valore deve essere [ e^-15; 1]. Ma, considerato il comportamento asintotico di ln(x), la radice di minor valore è praticamente x= e^-15.
Infatti f(e^-15)=(e^-15)²- ln(e^-15) -15= e^-30≃ 9.36·10^-14.
Non occorre applicare il metodo di bisezione.