N° 3 Geometria Solida

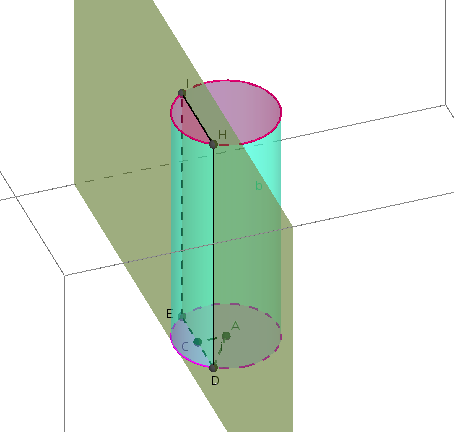
Considera un cilindro la cui base è un cerchio di raggio r e la cui altezza misura 5·r.

A quale distanza dall'asse del cilindro bisogna condurre un piano parallelo a tale asse

affinchè il quadrilatero che si ottiene come sezione del cilindro con tale piano abbia area 6·r² ?

Determina inoltre il volume dei due solidi che il piano divide. Disegna il solido.


Il quadrilatero è un rettangolo. L'altezza è 5r. È posto $x = \bar{AC}$ La base è : $\bar{ED} = 2 \cdot \sqrt{{\bar{AD}}^{2} - {\bar{AC}}^{2}} = 2 \cdot \sqrt{r^{2} - x^{2}}$ L'area della sezione è: $S = \bar{ED} \cdot \bar{HD} = 2 \cdot \sqrt{r^{2} - x^{2}} \cdot 5 r = 10 r \cdot \sqrt{r^{2} - x^{2}} = 6 \cdot r^{2}$ Da cui x: $100 \cdot (r^{2} - x^{2}) = 36 \cdot r^{2} \to 100 \cdot r^{2} - 100 \cdot x^{2} = 36 \cdot r^{2} \to 100 \cdot x^{2} = 64 \cdot r^{2} \to x = \frac{8}{10} \cdot r = \frac{4}{5} \cdot r$ Per i volumi occorre calcolare l'area del segmento circolare $\overset{︵}{ED}$ che può, a sua volta, essere calcolata come differenza tra l'area del settore circolare $\overset{︵}{DAE}$ e del triangolo $D \overset{Δ}{A} E$ . L'angolo $D \hat{A} E$ è : $D \hat{A} E = 2 \cdot \arccos \frac{\bar{AC}}{\bar{AD}} = 2 \cdot \arccos (\frac{4}{5})$ L'area del settore circolare è: $S_{\overset{︵}{DAE}} = \frac{{\bar{AD}}^{2} D \hat{A} E}{2} = r^{2} \cdot \arccos (\frac{4}{5})$

L'area del triangolo $D \overset{Δ}{A} E$ è :

$S_{DAE} = \frac{\bar{ED} \cdot \bar{AC}}{2} = \frac{2 \sqrt{r^{2} - x^{2}}}{2} \cdot \frac{4 r}{5} = \frac{4}{5} r \cdot \sqrt{r^{2} - \frac{16}{25} r^{2}} = \frac{4}{5} r \cdot \frac{3}{4} \cdot r = \frac{3}{5} \cdot r^{2}$

Quindi l'area del segmento circolare è: $S_{\overset{︵}{ED}} = S_{\overset{︵}{DAE}} - S_{DAE} = r^{2} \cdot \arccos (\frac{4}{5}) - \frac{3}{5} \cdot r^{2} = [\arccos (\frac{4}{5}) - \frac{3}{5}] \cdot r^{2}$

Adesso si può calcolare il volume del solido la cui base è il segmento circolare $\overset{︵}{ED}$ :

$V_{\overset{︵}{ED}} = \bar{HD} \cdot S_{\overset{︵}{ED}} = 6 \cdot [\arccos (\frac{4}{5}) - \frac{3}{5}] r^{3}$

L'altro volume per differenza con il volume del cilindro:

$V = 25 π {\cdot r}^{3} - V_{\overset{︵}{ED}} = [25 π - 6 \cdot \arccos (\frac{4}{5}) + \frac{18}{5}] \cdot r^{3}$