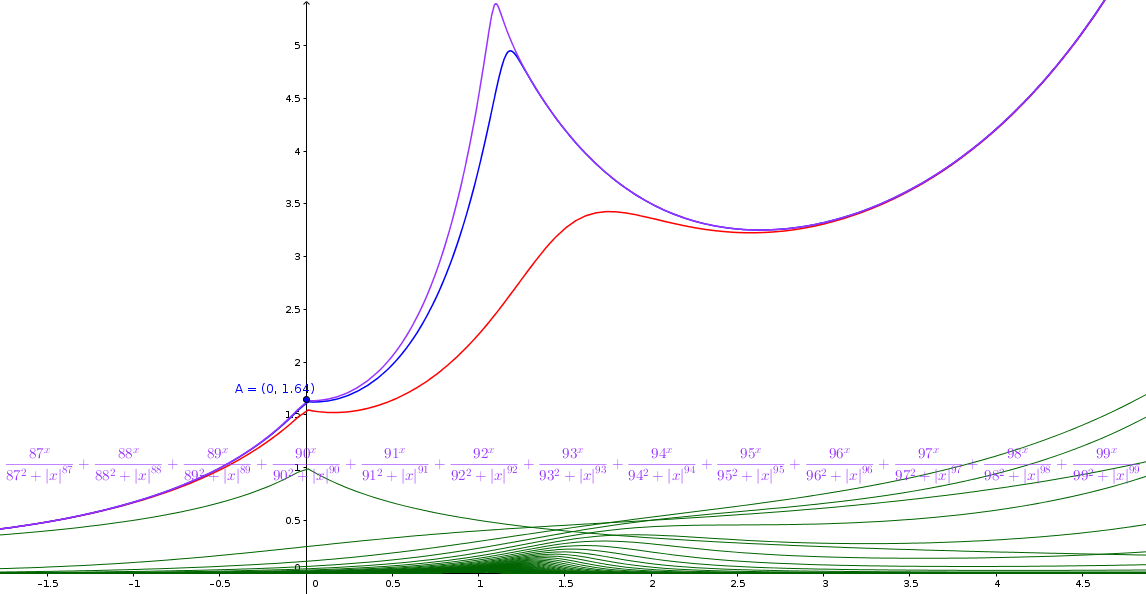
La successione dei temini della serie fino a n=100 e le somme parziali per n=10 (rosso), n=50 (blu), n= 100(viola)
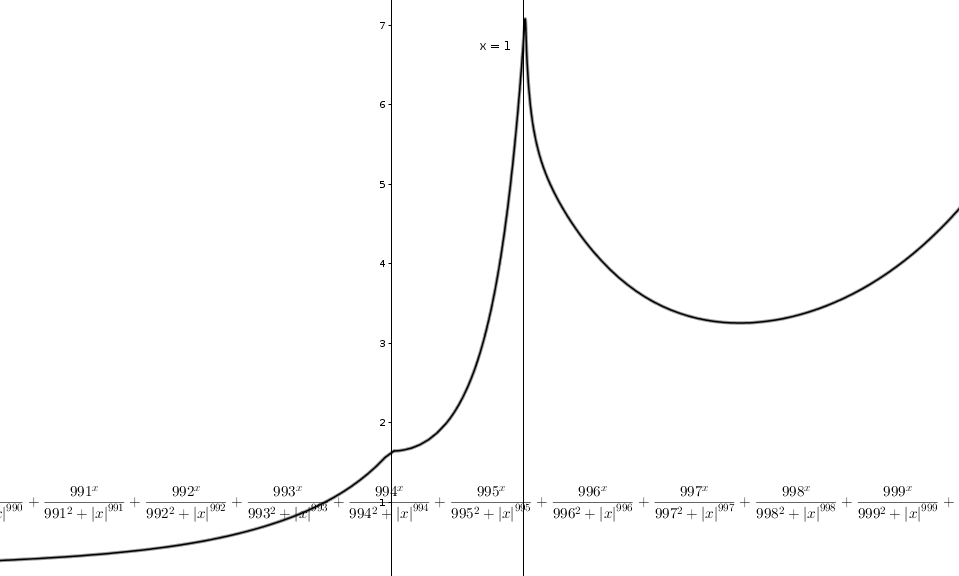
La somma parziale per n= 1000. Si noti la non continuità nel punto
x=1
e determinare se tale serie converge uniformemente nell'intervallo [-½,½].
Verifichiamo la condizione necessaria.
Se x=0 la serie diventa: ed è convergente.
Se x>1 il termine n-esimo della serie e ed è quindi soddisfatta la condizione necessaria.
Infatti che è uguale a zero se x>1.
Inoltre se x>1
Se x=1 che non converge.
Se 0<x<1 se 2 - x > 0 ⇒x < 2 ma è vero perchè 0 < x < 1
Se x<0 il temine della serie diventa e per qualunque x < 0 : ed è soddisfatta la condizione necessaria.
Quindi la serie non converge per x= -1
Se , poichè . Poichè l'esponente della serie numerica è maggiore di 1 allora, per il Criterio di Weierstrass, la serie converge totalmente all'interno dell'intervallo ]-1,1] e quindi anche all'interno dell'intervallo [½,+½] . La convergenza totale implica quella uniforme.
La successione dei temini della serie fino a n=100 e le somme parziali per n=10 (rosso), n=50 (blu), n= 100(viola)
|
|