Può essere espressa nella forma:

$\sum _{n=1}^{\infty }\frac{{\mid x\mid }^{\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{n^{x+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$

Applicando il criterio della radice verifichiamo la convergenza puntuale:

$\underset{n\to +\infty }{lim}\sqrt[n]{\frac{{\mid x\mid }^{\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{n^{x+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}=\underset{n\to +\infty }{lim}\frac{{\mid x\mid }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{{\left(\sqrt[n]{n}\right)}^{x+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}=\sqrt{\mid x\mid }$

da cui se :

$\mid x\mid >1$ la serie non converge

$\mid x\mid =1$ si devono distinguere due casi: $\{\begin{array}{c}x=1\to \sum _{n=1}^{\infty }\frac{1}{n^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\\ x=-1\to \sum _{n=1}^{\infty }\sqrt{n}\end{array}$nel primo caso la serie converge, nel secondo diverge.

-1<x<-1 la serie converge

Per $\mid x\mid <1$ si può osservare che: $\frac{{\mid x\mid }^{\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{n^{x+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}<\frac{1}{n^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$ e, poichè la serie numerica $\sum _{n=1}^{\infty }\frac{1}{n^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$ converge allora in questo intervallo la serie data converge totalmente e ciò implica anche la convergenza uniforme.

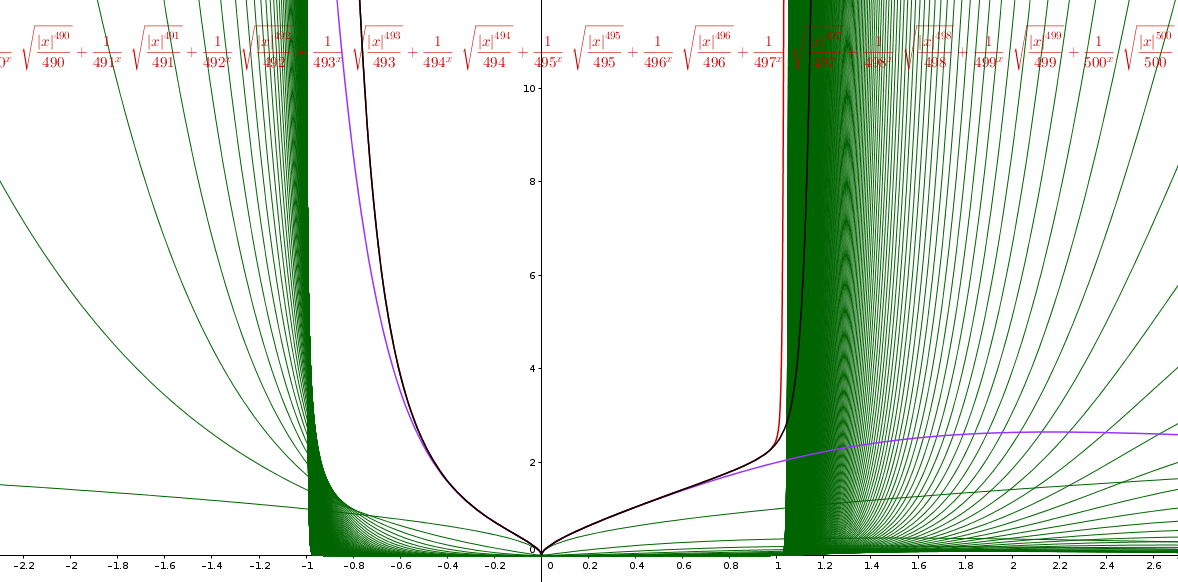
Nella figura la successione delle funzioni e la somma parziale per n=10 (viola), n=100 (nero), n=500 (rosso)

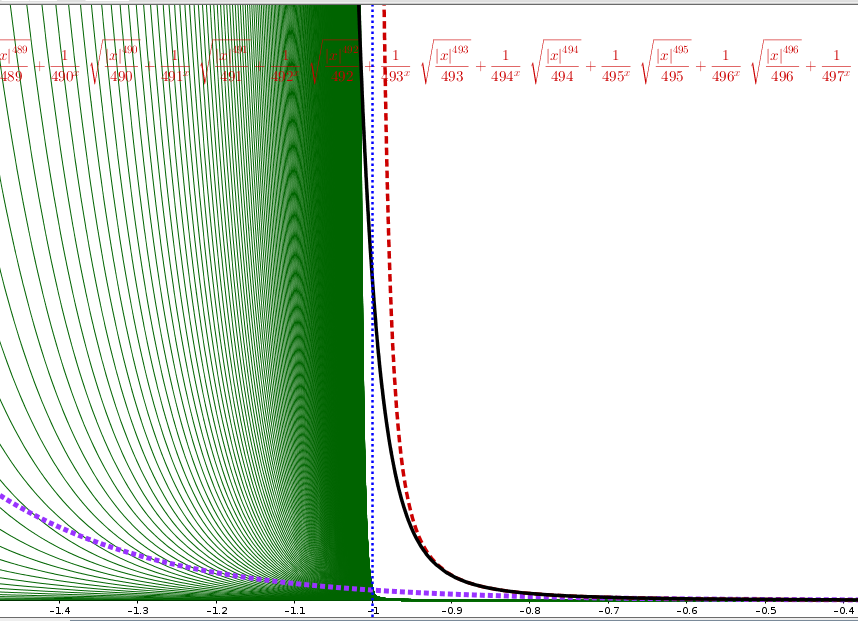
Nella figura particolare del precedente grafico in x=-1 (in blu asintoto verticale x=-1)