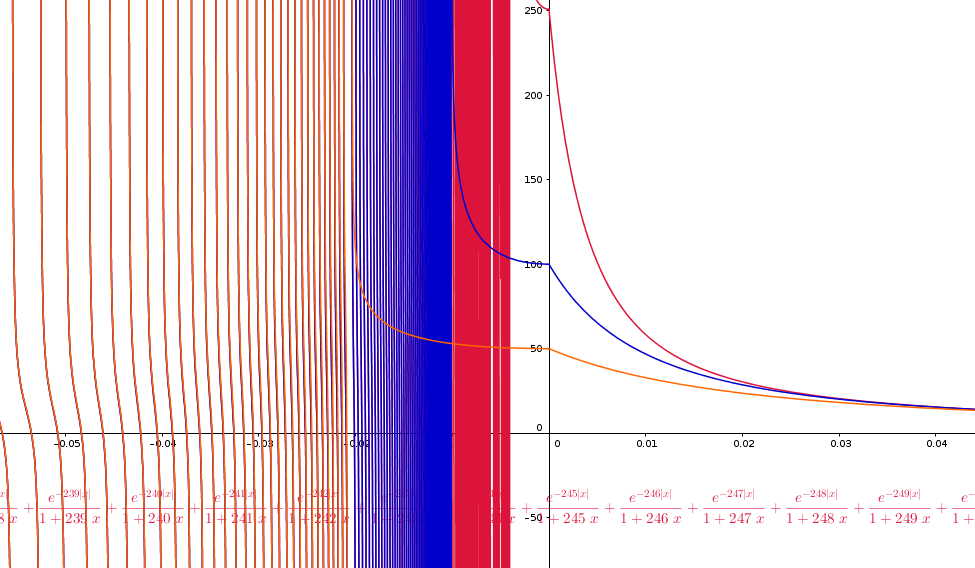
Le prime tre somme parziali per n= 50 (arancio), n= 100 (blu) e n=250 (rosso)
Verifica della condizione necessaria.
Se x= 0 il termine n-esimo diventa: , da cui e la serie non converge.
Se x> 0 , il limite ed è soddisfatta la condizione necessaria.
Se x<0, il limite ed è soddisfatta la conzione necessaria.
Se x> 0 vediamo se il = 0 . Applicando il criterio del rapporto per la convergenza delle successioni si ha:
Quindi da un certo punto in poi .
Poichè la serie armonica converge, per il criterio di Weierstrass, anche la serie converge totalmente e quindi anche uniformemente e puntualmente per x>0.
Se x <0 a serie può essere scritta nella forma: e in questo caso ci saranno infiniti punti di discontinuità prodotti dalla condizione: che tenderanno ad accumularsi verso lo zero da sinistra.
La serie non converge a nessuna funzione finita.
Le prime tre somme parziali per n= 50 (arancio), n= 100 (blu) e n=250 (rosso)
|