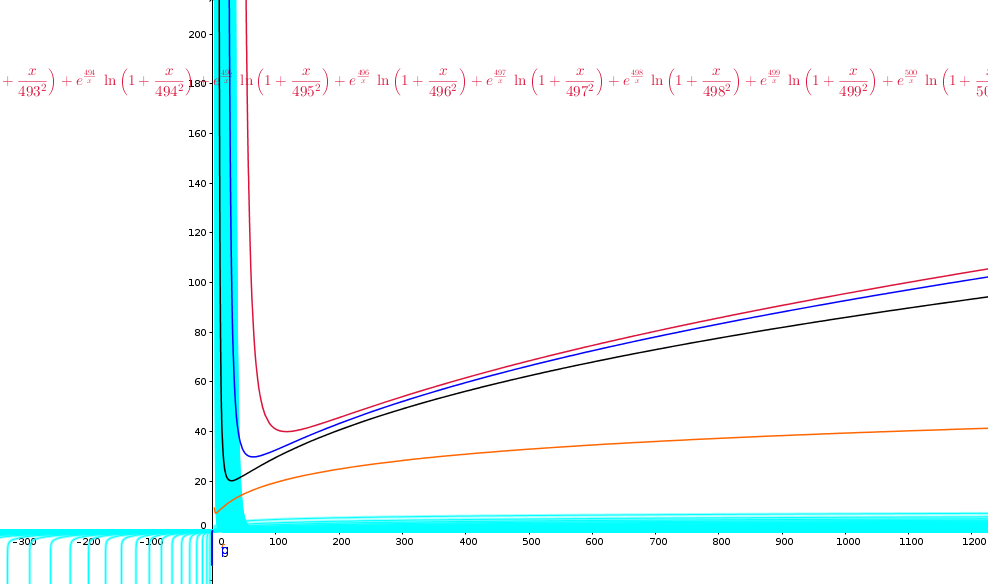
Nel grafico i termini della serie e le somme parziali fino n=10
(arancio) , n= 100 (nero), n=250 (blu) e n=500 (rosso)
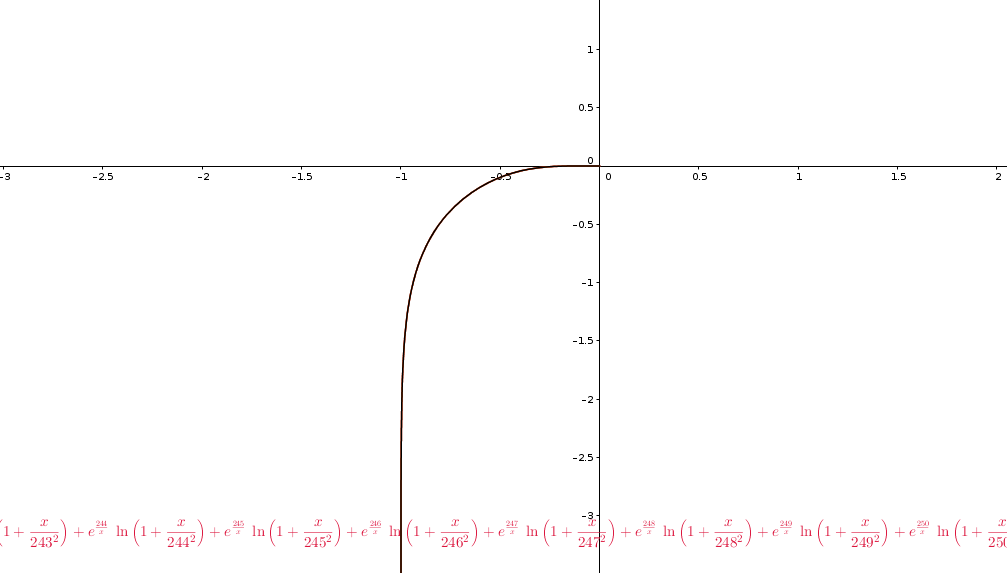
Nel grafico le somme parziali per x<0 per n=10, n=100 e n= 250 (indistinguibili perchè sovrapposte)
Verifichiamo la condizione necessaria.
Se x=0 il termine n-esimo diventa non definito e la serie non può convergere
Se x>0 poichè: :
(dove si è fatto uso dei limiti notevoli:
(n>0) e )
non è soddisfatta la condizione necessaria e quindi la serie data non converge.
Se x<0 bisogna considerare che possono esserci termini infiniti nelle somme parziali a causa della presenza del logaritmo. Anzi il primo termine, è definito per -1<x<0. Quindi in generale si può parlare di eventuale convergenza per -1<x<0.
Allora se -1<x<0 , ed è soddisfatta la condizione necessaria per la convergenza puntuale.
Ora consideriamo il limite:
( dove si è fatto uso del limite notevole: )
Quindi da un certo punto in poi .
Poichè la serie armonica converge, per il criterio di Weierstrass, anche la serie converge totalmente (e quindi anche uniformemente) per -1<x<0
 |
Nel grafico le somme parziali per x<0 per n=10, n=100 e n= 250 (indistinguibili perchè sovrapposte)
|