Verifichiamo la condizione necessaria.
Se x=0 la serie si annulla.
Se x≠0 , il ed è verficata la condizione necessaria.
Consideriamo ora il limite:
(dove si è fatto uso del limite notevole: con α>0).
Quindi, da un certo punto in poi,:
Poichè la serie armonica converge, per il criterio di Weierstrass, la serie converge totalmente per x≠ 0 e quindi anche uniformemente.
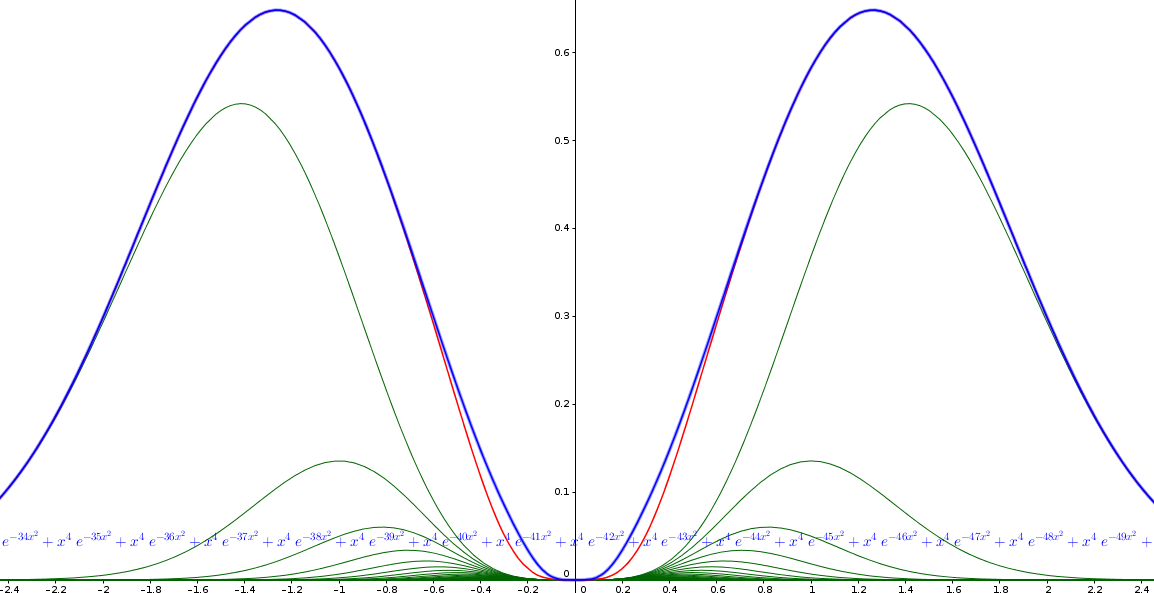
| Grafico
dei termini della serie fino a n=50 e delle somme parziali per n= 10
(rosso) e n= 50 (blu)
|