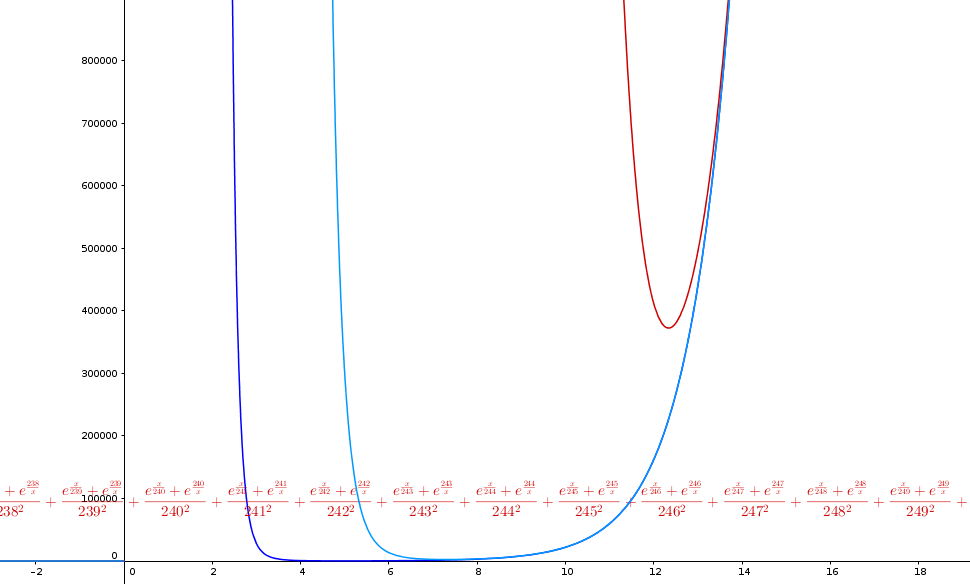
Le somme ridotte in x>0 con n= 50 (blu), n= 100 (celeste) ed n= 250 (rosso)
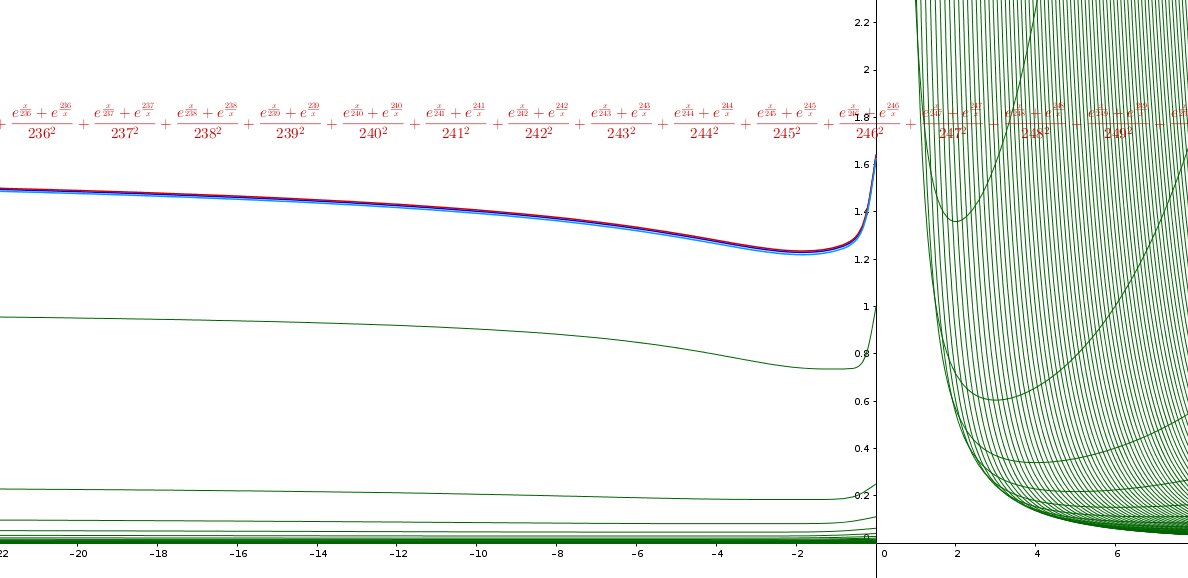
I termini della serie fino n= 250 (verde) e le somme ridotte per x<0 con n= 50, n= 100 e n=250 (quasi sovrapposte)
Verifichiamo la condizione necessaria.
Se x=0 il temini della serie non sono definiti.
Se x>0
(dove si è fatto uso del limite notevole ) e non è soddisfatta la condizione necessaria e quindi la serie data non converge.
Se x<0
è verificata la condizione necessaria.
Infine se x < 0 , poichè sia che si ha che , e poichè la serie armonica converge, per il criterio di Weierstrass, anche la serie converge totalmente (e uniformemente).
Le somme ridotte in x>0 con n= 50 (blu), n= 100 (celeste) ed n= 250 (rosso)
|
I termini della serie fino n= 250 (verde) e le somme ridotte per x<0 con n= 50, n= 100 e n=250 (quasi sovrapposte)
|