N. 4 SERIE DI POTENZE

Studiare, al variare di x∈ℝ, la convergenza della serie:

$\sum_{n = 1}^{\infty} {(1 + 3 n)}^{2} e^{n x}$

Posto

t = e^{x}

la serie diventa una serie di potenze :

\sum_{n = 1}^{\infty} {(1 + 3 n)}^{2} t^{n}

(con t≥0)

Il raggio di convergenza è: $\underset{n \to \infty}{R = lim} \frac{{(1 + 3 (n + 1))}^{2}}{{(1 + 3 n)}^{2}} = lim_{n \to \infty} {(\frac{1 + 3 n + 3}{1 + 3 n})}^{2} = lim_{n \to \infty} {(1 + \frac{3}{1 + 3 n})}^{2} = 1$

Per t=1 si ha: $\sum_{n = 1}^{\infty} {(1 + 3 n)}^{2}$ , si vede subito che la serie non converge.

Allora la serie converge puntualmente e assolutamente ∀t∈ [0,1[ e converge uniformemente ∀t∈ [0,r] ⊂ [0,1[

Non converge per t∈[1,+∞[.

Passando alle x, x= ln(t), , la serie data converge puntualmente e assolutamente ∀ x∈]-∞,0[ e uniformemente ∀x∈]-ln(r),+ln(r)[ con 0<r<1

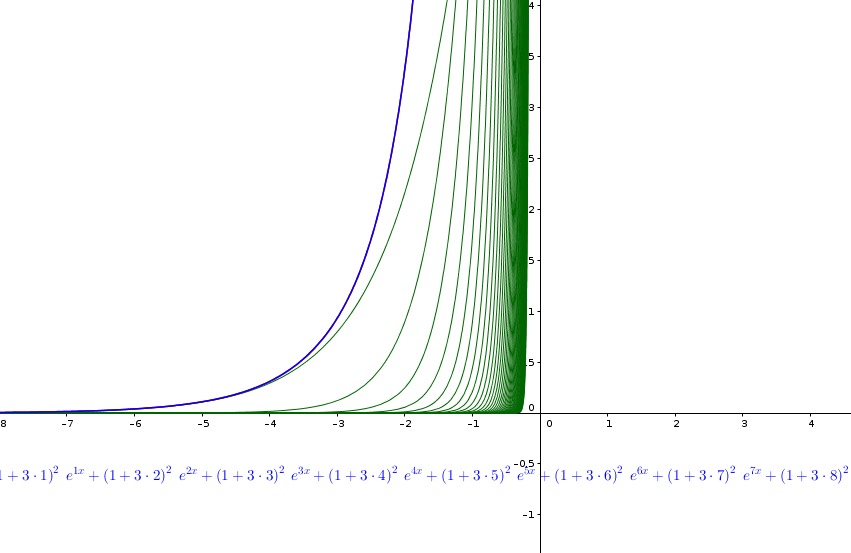
I termini della serie fino a n= 50 (verde) e le somme parziali per n= 10 (rosso) e n=50 (blu). La convergenza è molto rapida.