$\sum _{n=1}^{\infty }{\left(-1\right)}^{n+1}\frac{x^n}{n}$

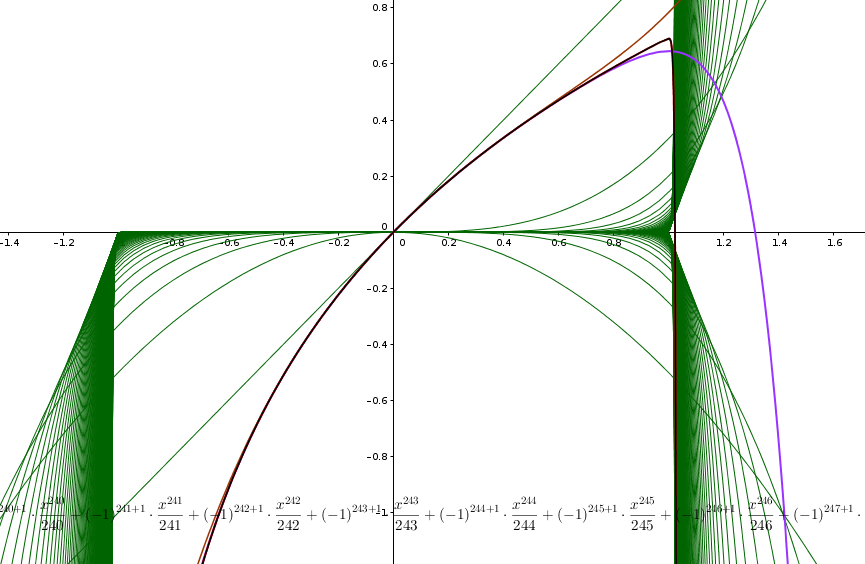
È una serie di potenze.

Il raggio di convergenza è: $R=\underset{n\to +\infty }{lim}\mid \frac{\raisebox{1ex}{${\left(-1\right)}^{n+2}$}\!\left/ \!\raisebox{-1ex}{$n+1$}\right.}{\raisebox{1ex}{${\left(-1\right)}^{n+1}$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}\mid =\underset{n\to +\infty }{lim}\frac{n}{n+1}=\underset{n\to +\infty }{lim}\frac{1}{1+\frac{1}{n}}=1$

Per x=1 si trova la serie numerica: $\sum _{n=1}^{\infty }{\left(-1\right)}^{n+1}·\frac{1}{n}$ che è una serie a termini alterni.

Poichè (Criterio di Leibniz):

1. $\underset{n\to +\infty }{lim}\frac{1}{n}=0$
2. $\frac{1}{n+1}\le \frac{1}{n}$ ∀ n∈ℕ

la serie numerica converge.

Per x= -1 si trova la serie numerica: $\sum _{n=1}^{\infty }{\left(-1\right)}^{n+2}·\frac{1}{n}$ che è una serie a termini alterni che, come visto prima, converge.

Allora la serie converge puntualmente e assolutamente ∀x∈ [-1,1] e converge uniformemente e totalmente ∀x∈ [-r,r] ⊂ [-1,1].

Non converge per x∈]-∞,1[∪]1,+∞[