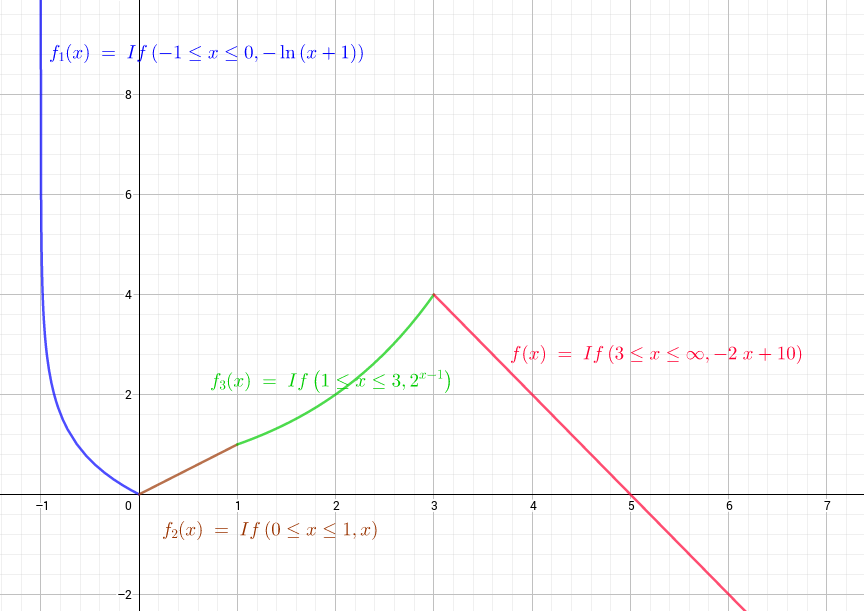N° 6 PROPRIETÀ FUNZIONI

f(x)=\begin{cases} -ln\left(x+1\right) & se\quad-1<x<0\\ x & se\quad0\le x<1\\ 2^{x-1} & se\quad1\le x<3\\ -2x+10 & se\quad x\ge3 \end{cases}

rappresentala in un piano cartesiano;

indica (dimostrandolo) in quali intervalli è decrescente e in quali intervalli è crescente;

determina i coefficienti b e c in modo che la funzione

g (x) = - x^{2} + b x + c

abbia come asse di simmetria x=3 e intersechi la

f (x)

nell'origine;

trova l'altro punto di intersezione tra

f (x)

g (x)

a. Rappresentazione della funzione :

Nell'intervallo ]-1,0] : $x_1<x_2⇒x_1+1<x_2+1⇒\ln\left({x_1+1}\right)<\ln\left({x_2+1}\right)⇒-\ln\left({x_1+1}\right)>-\ln\left({x_2+1}\right)⇒f(x_1)>f(x_2)$ decrescente.

Nell'intervallo [0,1]: $x_1<x_2⇒f(x_1)<f(x_2)c$
crescente.

Nell'intervallo [1,3[: $x_1<x_2⇒x_1-1<x_2-1⇒2^{x_1 - 1}<2^{x_2 - 1}⇒f(x_1)<f(x_2)$ crescente.

Nell'intervallo [3,∞[: $x_1<x_2⇒-2x_1>-2x_2⇒-2x_1+10>-2x_2+10⇒f(x_1)>f(x_2)$ decrescente.

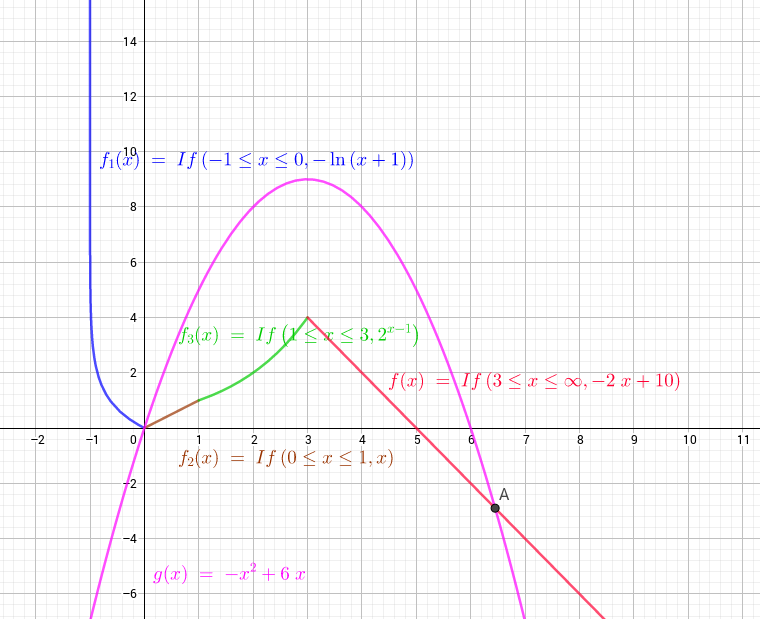
c. Se la funzione g(x) passa per l'origine deve essere c=0. La funzione rappresenta una parabola e l'asse di simmetria per la parabola è dato dall'espressione:

x=-\frac{b}{2a}⇒3=-\frac{b}{-2}⇒b=6

d. La parabola g(x) interseca l'asse delle ascisse in x= 0 e in x= 6 e ha vertice in (3,9) quindi interseca la funzione f(x) nel tratto rappresentato da f(x)=-2x+10. Troviamo l'ulteriore punto di intersezione:

-2x+10=-x^2+6x⇒x^2-8x+10=0⇒x=4±\sqrt{16-10}=4±\sqrt{6

L'altro punto di intersezione deve avere ascissa

x=4+\sqrt{6}

e ordinata

y=-2\left(4+\sqrt{6}\right)+10=2-2\sqrt{6}