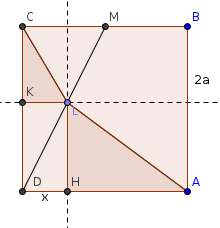
LIMITI E GEOMETRIA EUCLIDEA- Nel quadrato ABCD di lato 2a, sia M il punto medio di BC. Preso un punto L sul segmento DM, indica con H e K le proiezioni di L rispettivamente sui lati AD e DC. Determina il rapporto fra le aree dei triangoli ALH e LHC e calcolane il limite al tendere di L a D. (R: 2)
-
Assegnato
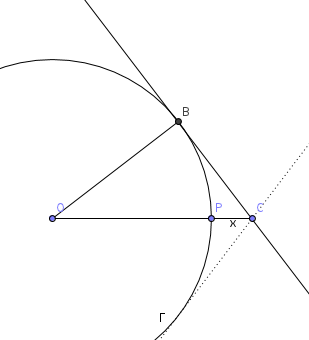
un segmento OC = a, si prenda un punto P su OC e si tracci la
circonferenza Γ con centro O e raggio OP ; da C si tracci una delle
tangenti a Γ, e sia B il punto di tangenza. Calcolare, al tendere di P
a C, il limite del rapporto (OC − OB − BC)/PC. (R: -∞)
- LIMITI E GEOMETRIA ANALITICA
- Considera la parabola di equazione y=4x - x² che interseca l'asse delle ascisse
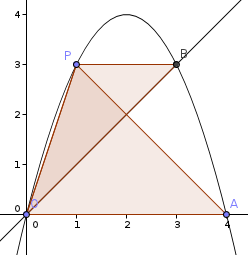nei punti O ed A e la bisettrice del primo
quadrante che incontra la parabola nei punti O e B. Detto P un punto
dell'arco di parabola OB determina il limite del rapporto delle aree dei triangoli OPB e OPA al tendere di P ad O. (R: 9/16)
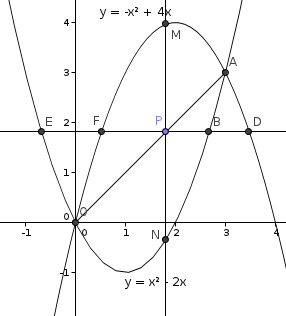
- Date le due parabole di equazioni y = −x² + 4x e y = x² − 2x, aventi in comune i punti O ed A, sia P un punto del segmento OA. Condotte da P le parallele agli assi cartesiani, siano E ed F i punti di minore ascissa in cui la parallela all’asse x taglia, rispettivamente, le due curve, e siano M ed N i punti in cui la parallela all’asse y taglia le due curve. Calcolare il limite del rapporto EF/M N al tendere di P ad O. (R: 1/8)
- LIMITI E TRIGONOMETRIA
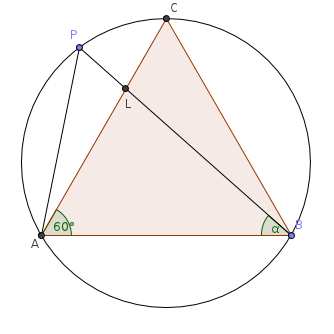
- Sia ABC un triangolo equilatero inscritto in una circonferenza di raggio r; considerato un punto P sull'arco AC della circonferenza e indicato con L il punto di intersezione fra le corde PB e AC, determina il limite di (AL + LP)/AP al tendere di P ad A. (AP, AL e LP sono lunghezze di segmenti). (R: 2)
-
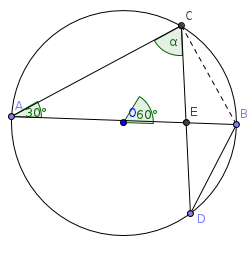
In una circonferenza di diametro AB = 2r sia C il punto tale che risulti BAC = π/6 e sia D un punto generico appartenente alla semicirconferenza non contenente C. Indicato con E il punto che la corda CD ha in comune con il diametro AB, calcolare il limite del rapporto (EB + ED)/BD al tendere di D a B. (R: √3)