Interpolazione

INTERPOLAZIONE DI DATI

L'interpolazione consiste nel processo utile a determinare la "migliore" stima dei valori di una funzione f(x) quando ci sono a disposizione solo un numero finito di punti noti. Se i dati a disposizione sono n+1 si dimostra in algebra che esiste un unico polinomio interpolatore di grado n che passa per tutti i punti, tuttavia questo, in calcolo numerico, è solitamente scelto in modo che interpoli solo alcuni dati e non tutti.
Anche se unico, il polinomio interpolatore può essere definito in modi diversi. Due possibili scelte sono il polinomio di Newton delle differenze divise e il polinomio di Lagrange.

IL METODO DI NEWTON DELLE DIFFERENZE DIVISE

INTERPOLAZIONE LINEARE. È la forma più semplice di interpolazione: connette due dati con una retta e la usa per stimare i valori della funzione nei punti intermedi.
Dalla similitudine dei due triangoli:

$\frac{f_1(x)-f(x_0)}{x-x_0}=\frac{f(x_1)-f(x_0)}{x_1-x_0}$ da cui, per esempio, : $f_1(x)=f(x_0)+\frac{f(x_1)-f(x_0)}{x_1-x_0}\left(x-x_0\right)$

INTERPOLAZIONE QUADRATICA. L'interpolazione lineare può introdurre notevoli errori nella stima dei valori della funzione per l'assenza di curvatura. Ma avendo a disposizione tre punti è possibile introdurre una curvatura del secondo ordine (parabola) per interpolare meglio i dati.
ll polinomio interpolatore quadratico di Newton è del tipo:

$f_2(x)=b_0+b_1\left(x-x_0\right)+b_2\left(x-x_0\right)\left(x-x_1\right)$
che può essere scritto nella forma:

$f_2(x)= a_0 + a_1x+a_2x^2$
i coefficienti si determinati dal sistema:

$\begin{cases} a_0=b_0-b_1x_0+b_2x_0x_1 \\ a_1=b_1-b_2x_0-b_2x_1\\ a_2=b_2 \end{cases}$

I punti devono essere molti vicini per avere una interpolazione lineare che si avvicina al valore vero.

E per trovare i coefficienti occorre imporre che il polinomio passi per i tre punti dati:

$\begin{cases} f(x_0)=b_0+b_1(x_0-x_0)+b_2(x_0-x_0)(x_0-x_1)=b_0 \\ f(x_1)=b_0+b_1(x_1-x_0)+b_2(x_1-x_0)(x_1-x_1)=b_0+b_1(x_1-x_0)\\f(x_2)=b_0+b_1(x_2-x_0)+b_2(x_2-x_0)(x_2-x_1) \end{cas$

la soluzione del sistema è: $\begin{cases} b_0=f(x_0) \\ b_1=\frac{f(x_1)-f(x_0)}{x_1-x_0} \\ b_2=\frac{\frac{f(x_2)-f(x_1)}{x_2-x_1}-\frac{f(x_1)-f(x_0)}{x_1-x_0}}{x_2-x_0}\end{cases}$
e per la forma dei coefficienti il metodo è detto delle differenze divise.
La forma finale del polinomio interpolatore è:

$f_2(x)=f(x_0)+\frac{f(x_1)-f(x_0)}{x_1-x_0}\left(x-x_0\right)+\frac{\frac{f(x_2)-f(x_1)}{x_2-x_1}-\frac{f(x_1)-f(x_0)}{x_1-x_0}}{x_2-x_0}(x-x_0)(x-x_1)$

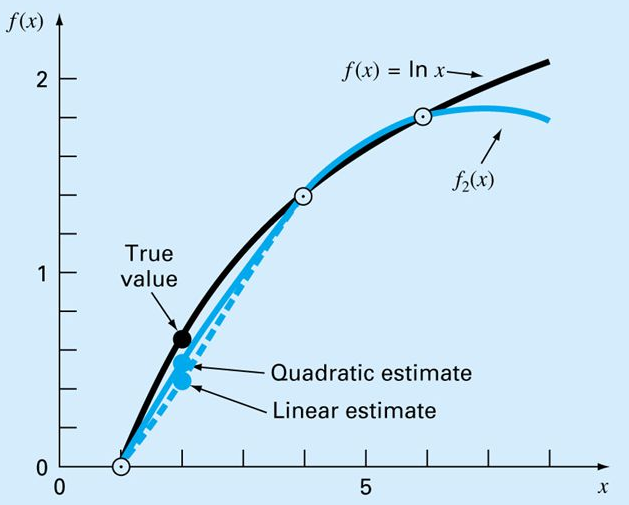
e si vede che è un'estensione del polinomio di interpolazione lineare con l'inclusione del termine del secondo ordine.

I POLINOMI INTERPOLANTI DI NEWTON DI GRADO n . La formula generale per un polinomio di ordine n passante per n+1 punti è:

f_n(x)=b_0+b_1(x-x_0)+b_2(x-x_0)(x-x_1)+ ... + b_n(x-x_0)(x-x_1)(x-x_2) ⋅⋅⋅(x-x_{n-1})

dove i coefficienti (differenze divise) valgono: $\begin{cases} b_0=f(x_0) \\b_1=\frac{f(x_1)-f(x_0)}{x_1-x_0} \\b_2=\frac{\frac{f(x_2)-f(x_1)}{x_2-x_1}-\frac{f(x_1)-f(x_0)}{x_1-x_0}}{x_2-x_0}\\b_3=\frac{\frac{\frac{f(x_3)-f(x_2)}{x_3-x_2}-\frac{f(x_2)-f(x_1)}{x_2-x_1}}{x_3-x_1}-\frac{\frac{f(x_2)-f(x_1)}{x_2-x_1}-\frac{f(x_1)-f(x_0)}{x_1-$ la loro forma diventa sempre più complessa.

Se introduciamo la notazione : $f\left[x_n,x_{n-1}, ...., x_1,x_0\right]=\frac{f\left[x_n,x_{n-1}, ...,x_1\right]-f\left[x_{n-1},...,x_1,x_0\right]}{x_n-x_0}$ possono essere scritti nella forma ricorsiva, più astratta e compatta, :

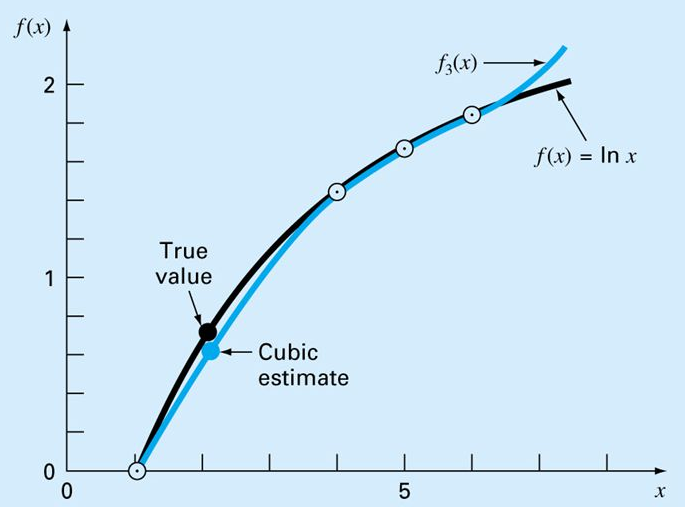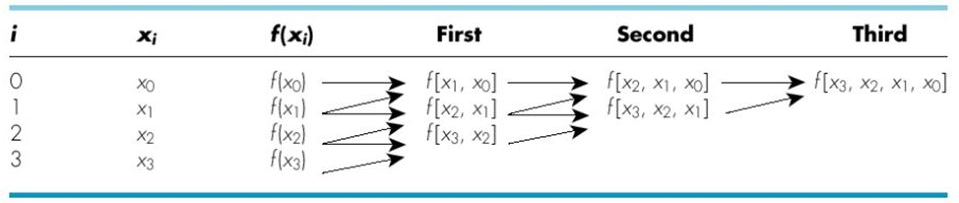\begin{cases} b_0=f\left[x_0\right] \\ b_1=f\left[x_1,x_0\right]\\b_2=f\left[x_2,x_1,x_0\right] \\ ...\\b_n=f\left[x_n,x_{n-1},...,x_1,x_0\right]\end{cases

A sinistra interpolazione cubica di ln(x). Qui sopra, schema per la generazione ricorsiva delle differenze divise

L' ERRORE PER I POLINOMI INTERPOLANTI DI NEWTON.

La formula dei polinomi di Newton è simile alla formula dell'espansione di Taylor, in cui si aggiungono via via derivate agli ordini più alti della funzione. Quindi l'errore di troncamento può essere definito come nel caso dell'espansione di Taylor:

R_n= \frac{f^{n+1}\left(ξ\right)}{\left(n+1\right)!}\left(x-x_0\right)\left(x-x_1\right)⋅⋅⋅\left(x-x_n\right)

dove ξ è un punto appartenente all'intervallo dei dati. Tuttavia, in questo modo, non è possibile calcolare l'errore perché richiede la conoscenza della forma analitica della funzione che non possediamo.
Un modo alternativo è stimare l'errore utilizzando la differenza divisa di ordine n+1:

R_n=f\left[x,x_n,x_{n-1},....,x_0\right]\left(x-x_0\right)\left(x-x_1\right)⋅⋅⋅\left(x-x_n\right)

anche se per la sua valutazione è necessario possedere un punto in più, x_n+1:

R_n≃f\left[x_{n+1},x_n,x_{n-1},....,x_0\right]\left(x-x_0\right)\left(x-x_1\right)⋅⋅⋅\left(x-x_n\right)

e il metodo più rapido per valutarlo è come differenza tra la stima successiva e la stima attuale:

R_n=f_{n+1}(x)-f_n(x)

L' INTERPOLAZIONE POLINOMIALE DI LAGRANGE

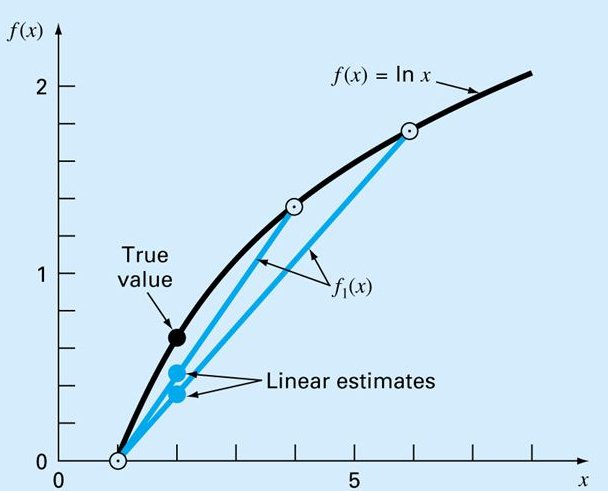
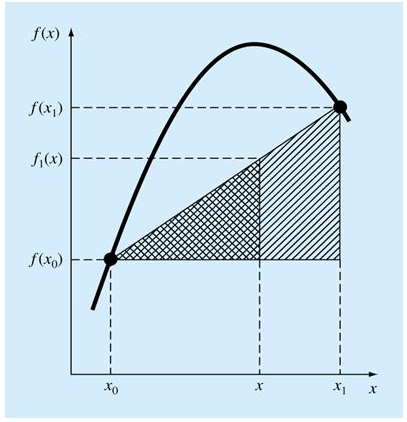
È una riformulazione dei polinomi di Newton delle differenze divise molto più coincisa che evita il calcolo di dividere le differenze.
La forma generale è :

f_n\left(x\right)=\sum_{i=0}^n\,L_i(x)f(x_i)\quad \qquad L_i(x)={\product_{j=0}^n}_{i≠j}\frac{x-x_j}{x_i-x_j}

Per n=1:

f_1(x)=\frac{x-x_1}{x_0-x_1}f(x_0)+\frac{x-x_0}{x_1-x_0}f(x_1)

Si può facilmente comprendere l'origine della formula per n=1 se si considerano due punti (x₀;f(x₀)), (x₁;f(x₁)) e un terzo punto compreso di cui si sceglie l'ascissa x e si vuole conoscere la f(x) per interpolazione ma che chiamiamo f₁(x).
Imponiamo:

\frac{f(x_1)-f_1(x)}{x_1-x}=\frac{f_1(x)-f(x_0)}{x-x_0}

ovvero che i coefficienti angolari delle rette passanti per (x₀;f(x₀)) e (x;f₁(x)) e per (x₁;f(x₁)) e (x;f₁(x)) siano uguali. Dopo alcuni passaggi si può ricavare la formula di interpolazione polinomiale di Lagrange per n=1.

Per n= 2 si cerca una parabola che passi per x₀, x e x₂ e una parabola che passi per x₀, x e x₁ e si impone che siano le stesse parabole.
Si trova:

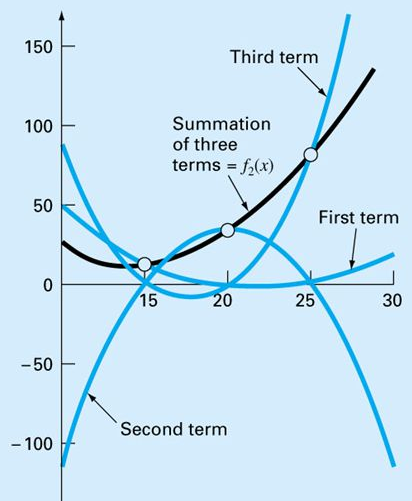
f_2(x)=\frac{\left(x-x_1\right)\left(x-x_2\right)}{\left(x_0-x_1\right)\left(x_0-x_2\right)}f(x_0)+\frac{\left(x-x_0\right)\left(x-x_2\right)}{\left(x_1-x_0\right)\left(x_1-x_2\right)}f(x_1)+\frac{\left(x-x_0\right)\left(x-x_1\right)}{\left(x_2-x_0\right)\left(x_2-x_1\right)}f(x_2)

In questo ultimo caso ognuno dei tre termini diventa un polinomio di secondo grado che passa attraverso uno dei tre punti ed è zero in corrispondenza degli altri due punti. La somma dei tre polinomi è un polinomio di secondo grado che passa esattamente attraverso i tre punti dati.

CONFRONTO FRA I DUE METODI:

Il metodo di Newton è preferibile per calcoli esploratori (quando n non è conosciuto a priori):
il metodo di Newton ha vantaggi dovuti alla sua similitudine con la serie di Taylor;
la stima dell'errore con i polinomi di Newton può essere facilmente implementata perché utilizza le differenze finite;
il metodo di Lagrange è preferibile quando soltanto un'interpolazione è richiesta (cioè quando l'ordine n è conosciuto a priori);
il metodo di Lagrange è più leggero dal punto di vista computazionale.

L'ESTRAPOLAZIONE

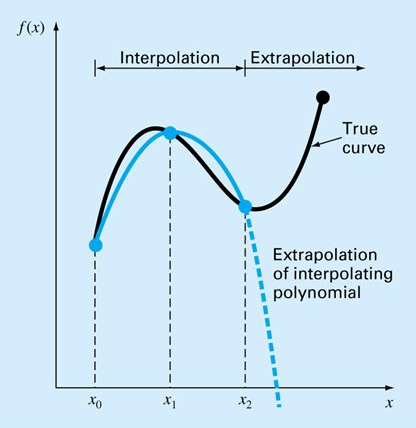
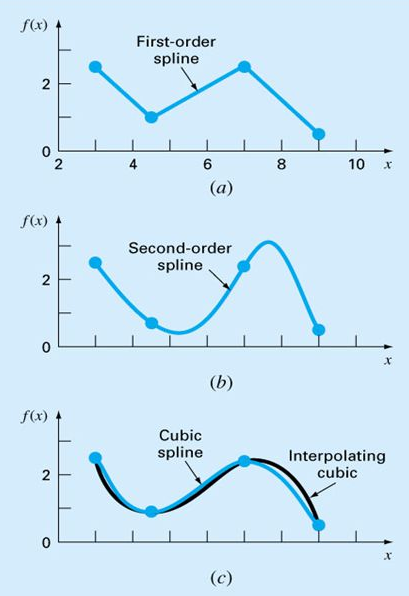
L'estrapolazione è il processo che permette di calcolare f(x) per un valore di x al di fuori dell'intervallo conosciuto dei punti x₀, x₁, ...., x_n. Bisogna porre molta attenzione nel processo di estrapolazione perché se il valore di x estrapolato non è vicino ai punti a disposizione si può commettere un errore molto grande.

L'INTERPOLAZIONE CON SPLINE

A volte l'interpolazione con polinomi di grado elevato può dare risultati poco affidabili, specialmente se si hanno bruschi cambiamenti della funzione. In figura a destra, lettere (a), (b) e (c) sono riportate tre interpolazioni su 4, 6 e 8 nodi di una funzione a gradino. Come si vede nel caso (c) l'interpolazione su più nodi non migliora l'interpolazione della funzione.

Un approccio alternativo è applicare un polinomio di grado inferiore ad un sottoinsieme di nodi usando vincoli ai valori delle derivate della funzione nei nodi.

Questo polinomio di grado inferiore è detto funzione spline (vedi figura a destra lettera (d)), il metodo si dice interpolazione spline (dal nome inglese del curvilineo flessibile usato per l’interpolazione meccanica di una serie di dati)

SPLINE LINEARE O DI PRIMO ORDINE. In questo caso ogni coppia di nodi sono connessi con un segmento di retta. Per ogni intervallo: $f(x)=f(x_i) + m_i\left(x-x_i\right)$ con: $m=\frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}$ Quindi la spline lineare è identica alla interpolazione lineare e non offre alcuna novità rispetto all'interpolazione lineare. Inoltre la derivata prima è discontinua nei nodi. In generale per garantire che la derivata di ordine m sia continua occorre usare una interpolazione con un polinomio spline di grado m+1.

SPLINE QUADRATICA. Nella spline quadratica ogni intervallo è interpolato con un diverso polinomio di secondo grado. Per n+1 punti ci sono n intervalli quindi n polinomi: $\begin{cases} f(x_1)=a_1x_1^2+b_1x_1+c_1 \\ ⋯\\ f(x_i)=a_ix_i^2+b_ix_i+c_i \\...\\ f(x_n)=a_nx_n^2+b_nx_n+c_n\end{cases$

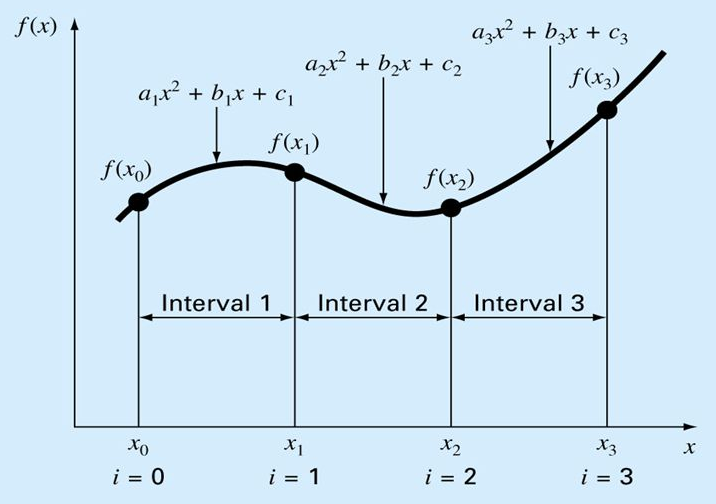
Occorre trovare 3n coefficienti incogniti ma bisogna imporre delle condizioni:

Due polinomi adiacenti devono passare per i punti interni. 2(n-1) equazioni per i= 2,..., n punti: $f(x_{i-1})= a_{i-1}x_{i-1}^2+b_{i-1}x_{i-1}+c_{i-1}$ $f(x_{i-1})= a_{i}x_{i-1}^2+b_{i}x_{i-1}+c_{i}$
Poiché ci sono n-1 punti interni questa condizione produce 2(n-1) equazioni

Il primo e l'ultimo polinomio devono passare per i punti iniziale e finale:

$f(x_{0})= a_{1}x_{0}^2+b_{1}x_{0}+c_{1}$ $f(x_{n})= a_{n}x_{n}^2+b_{n}x_{n}+c_{n}$
Altre due equazioni. In totale 2n equazioni.

Le derivate prime sinistra e destra nei punti interni devono essere uguali (continuità della derivata prima). (n-1) equazioni per i= 2,..., n punti:

$f'(x_{i-1})=2a_{i-1}x_{i-1}+b_{i-1}=2a_{i}x_{i-1}+b_{i}$
Poiché ci sono n-1 punti interni questa condizione produce (n-1) equazioni

Così abbiamo 2n + n - 1 = 3n - 1 equazioni, ne serve un'altra. L'ultima equazione è scelta in modo arbitrario.
Uno modo potrebbe essere imporre che la derivata seconda nel primo punto sia zero. Questa scelta equivale ad imporre che a₁=0. A proposito bisogna sottolineare che la continuità della derivata seconda nei nodi non è garantita.

SPLINE CUBICA. Nella spline cubica ogni intervallo è rappresentato da un diverso polinomio di terzo grado:

$f(x)=a_ix^3+b_ix^2+c_ix+d_$
In questo caso ci sono 4n coefficienti da trovare per n+1 punti.
Le condizioni sono:

Due polinomi adiacenti devono passare per i punti interni: 2n - 2 equazioni;

Il primo e l'ultimo polinomio devono passare per i punti iniziale e finale: 2 equazioni;

Le derivate prime sinistre e destre nei punti interni devono essere uguali: n - 1 equazioni;

Le derivate seconde sinistre e destre nei punti interni devono essere uguali: n - 1 equazioni;

Le derivate seconde nei punti iniziale e finale sono assunte nulle (queste condizioni sono una scelta detta dello spline naturale): 2 equazioni

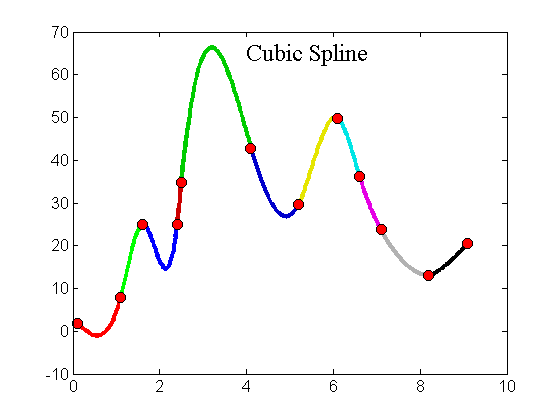Questa volta è garantita la continuità della derivata seconda nei nodi ma non della derivata terza.

Le precedenti condizioni forniscono un sistema di 4n equazioni a 4n incognite che, risolto, produce i 4n coefficienti delle n funzioni di terzo grado che interpolano ogni intervallo, tuttavia è un sistema molto grande. Ma esiste la possibilità di ridurlo. Poiché il polinomio è una cubica e la sua derivata seconda è una retta, possiamo rappresentare questa, tra due nodi, come un polinomio di Lagrange al primo ordine:

$f_i''(x)=f''(x_{i-1})\frac{x-x_i}{x_{i-1}-x_i}+f''(x_i)\frac{x-x_{i-1}}{x_i-x_{i-1}}$
possiamo poi ricavare la funzione primitiva (che cerchiamo) integrando due volte introducendo però due costanti di integrazione. La prima integrazione produce la derivata prima:

$f_i'(x)=f''(x_{i-1})\frac{\left(x-x_i\right)^2}{2\left(x_{i-1}-x_i\right)}+f''(x_i)\frac{\left(x-x_{i-1}\right)^2}{2\left(x_i-x_{i-1}\right)}+C_i$
La seconda integrazione produce la funzione primitiva:

$f_i(x)=f''(x_{i-1})\frac{\left(x-x_i\right)^3}{6\left(x_{i-1}-x_i\right)}+f''(x_i)\frac{\left(x-x_{i-1}\right)^3}{6\left(x_i-x_{i-1}\right)}+C_ix+D_i$
Le costanti vengono fissate in modo tale che la funzione assuma i valori noti nei nodi x_i e x_i-1:

$\begin{cases} f_i(x_i)=f''(x_i)\frac{\left(x_i-x_{i-1}\right)^3}{6\left(x_i-x_{i-1}\right)}+C_ix_i+D_i=\frac{f''(x_i)}{6}\left(x_i-x_{i-1}\right)^2+C_ix_i+D_i \\ f_i(x_{i-1})=f''(x_{i-1})\frac{\left(x_{i-1}-x_i\right)^3}{6\left(x_{i-1}-x_i\right)}+C_ix_{i-1}+D_i =\frac{f''(x_{i-1})}{6}\left(x_{i-1}-x_{i}\right)^2+C_ix_{i-1}+D_i \end{cases}$
Se si ricavano C_i e D_i si trova il polinomio di terzo grado tra il nodo x_i-1 e x_i :

$f_i(x)=\frac{f''(x_{i-1})}{6\left(x_i-x_{i-1}\right)}\left(x_i-x\right)^3+\frac{f''(x_{i})}{6\left(x_i-x_{i-1}\right)}\left(x-x_{i-1}\right)^3+$ $+ \left[\frac{f(x_{i-1})}{\left(x_i-x_{i-1}\right)}-\frac{f''(x_{i-1})\left(x_i-x_{i-1}\right)}{6}\right]\left(x_i-x\right)+\left[\frac{f(x_i)}{\left(x_i-x_{i-1}\right)}-\frac{f''(x_i)\left(x_i-x_{i-1}\right)}{6}\right]\left(x-x_{i-1}\right)$
servono però i valori delle derivate seconde in n - 1 nodi (ricordarsi, nella spline naturale, che f''(x₀) = f''(x_n) = 0 ).
Se, trovate le costanti di integrazione C_i , si ricava l'espressione della derivata prima e si impone la continuità della derivata prima in ogni polo si ottiene il sistema lineare (n - 1)·(n - 1):

$\left(x_i-x_{i-1}\right)f''(x_{i-1})+2\left(x_{i+1}-x_{i-1}\right)f''(x_i)+\left(x_{i+1}-x_i\right)f''(x_{i+1})=\frac{6}{\left(x_{i+1}-x_i\right)}\left[f(x_{i+1})-f(x_i)\right]+\frac{6}{\left(x_{i}-x_{i-1}\right)}\left[f(x_{i-1})-f(x_i)\right]$
che risolto fornisce le derivate seconde negli n-1 poli. Notare che ci sono solo tre incognite (derivate seconde) in ogni equazione e che la matrice dei coefficienti è una matrice tridiagonale.