Numerical Differentiation

DERIVAZIONE NUMERICA

DERIVATA PRIMA

Partendo dall'espansione di Taylor intorno al punto x_i:

f(x_{i+1})=f(x_i) +f'(x_i)h+\frac{f''(x_i)}{2}h^2+O(h^3)

(1)

Si può calcolare la derivata prima:

f'(x_i)=\frac{f(x_{i+1})-f(x_i)}{h}-\frac{f''(x_i)}{2}h+O(h^2)

formula che suggerisce di approssimare la derivata prima con il rapporto incrementale, calcolato per h molto piccolo, :

f'(x_i)=\frac{f(x_{i+1})-f(x_i)}{h}+O(h

con

O(h)=\frac{Mh}{2}

, M è il valore massimo della derivata seconda all'interno dell'intervallo [x_i , x_i+1].
Questa è la "first forward approximation" o "formula delle differenze finite in avanti".
È possibile fare un'espansione di Taylor all'indietro:

f(x_{i-1})=f(x_i) -f'(x_i)h+\frac{f''(x_i)}{2}h^2+O(h^3)

(2)

da cui si ottiene la "first backward approximation" o formula delle differenze finite all'indietro:

f'(x_i)=\frac{f(x_i)-f(x_{i-1})}{h} +O(h)

Sommando la forward approximation e la backward approximation si ottiene:

2f'(x_i)=\frac{f(x_{i+1})-f(x_i)}{h}-\frac{f''(x_i)}{2}h-\frac{f'''(x_i)}{6}h^2+\frac{f(x_{i})-f(x_{i-1})}{h}+\frac{f''(x_i)}{2}h-\frac{f'''(x_i)}{6}h^2+O(h^3)⇒

⇒f'(x_i)=\frac{f(x_{i+1})-f(x_{i-1})}{2h}-\frac{f'''(x_i)}{6}h^2+O(h^3)=\frac{f(x_{i+1})-f(x_{i-1})}{2h}+O(h^2)

questa rappresenta la "first central approximation" con un errore proporzionale a h².

DERIVATA SECONDA E SUCCESSIVE

Partendo dall'espansione di Taylor intorno al punto x_i ma con passo 2h, si ottiene:

f(x_{i+2})=f(x_i)+f'(x_i) \cdot 2h + \frac{f''(x_i)}{2}(2h)^2+O(h^3)

Sottraendo da questa espansione il doppio espansione (1) (passo h) :

f(x_{i+2})-2f(x_{i+1})=f(x_i)+f'(x_i) \cdot 2h + \frac{f''(x_i)}{2}(2h)^2+O(h^3)-2\left(f(x_i) +f'(x_i)h+\frac{f''(x_i)}{2}h^2+O(h^3)\right)=-f(x_i)+f''(x_i)h^2+O(h^3)

Da cui:

f''(x_i)=\frac{f(x_{i+2})-2f(x_{i+1}) + f(x_i)}{h^2}+O(h)

Questa è l'approssimazione forward della derivata seconda.
Analogamente, espandendo con Taylor all'indietro, si ottiene l'approssimazione backward:

f''(x_i)=\frac{f(x_{i})-2f(x_{i-1}) + f(x_{i-2})}{h^2}+O(h)

Se sommiamo le due espansioni (1) e (2) una in avanti e l'altra all'indietro:

f(x_{i+1})+f(x_{i-1})=f(x_i)+f'(x_i)h+\frac{f''(x_i)}{2}h^2+\frac{f'''(x_i)}{6}h^3+O(h^4) + f(x_i) -f'(x_i)h+\frac{f''(x_i)}{2}h^2-\frac{f'''(x_i)}{6}h^3+O(h^4)=2f(x_i)+f''(x_i)h^2+O(h^4)

si ottiene:

f''(x_i)=\frac{f(x_{i+1})+f(x_{i-1})-2f(x_i)}{h^2}+O(h^2)

(3)

che è first central approximation della derivata seconda.

In modo analogo è possibile ricavare la formula centrata della derivata terza di ordine O(h²):

f'''(x_i)=\frac{f(x_{i+2})-2f(x_{i+1})+2f(x_{i-1})-f(x_{i-2})}{2h^3}+O(h^2)

e della derivata quarta di ordine O(h²):

f''''(x_i)=\frac{f(x_{i+2})-4f(x_{i+1})+6f(x_i)-4f(x_{i-1})+f(x_{i-2})}{h^4}+O(h^2)

FORMULE CON ERRORI AGLI ORDINI SUPERIORI

La first central approximation per la derivata prima è una formula a due punti che la approssima con un errore proporzionale a h². Per ottenere una first central approximation della derivata seconda occorre utilizzare tre punti: ogni volta che aumenta l'ordine di derivazione occorre un punto in più.
È possibile costruire formule centrate che, coinvolgendo un numero superiore di punti, permettono di approssimare le derivate con errore ancora minore ("second central approximation").
Scriviamo le espansioni di Taylor:

\begin{cases} f(x_{i+2})=f(x_i) +f'(x_i)2h+\frac{f''(x_i)}{2}4h^2+\frac{f'''(x_i)}{6}8h^3+\frac{f''''(x_i)}{24}16h^4+O(h^5) \\ f(x_{i+1})=f(x_i) +f'(x_i)h+\frac{f''(x_i)}{2}h^2+\frac{f'''(x_i)}{6}h^3+\frac{f''''(x_i)}{24}h^4+O(h^5) \\f(x_{i-1})=f(x_i) -f'(x_i)h+\frac{f''(x_i)}{2}h^2-\frac{f'''(x_i)}{6}h^3+\frac{f''''(x_i)}{24}h^4+O(h^5)\\f(x_{i-2})=f(x_i)-f'(x_i)2h+\frac{f''(x_i)}{2}4h^2-\frac{f'''(x_i)}{6}8h^3+\frac{f''''(x_i)}{24}16h^4+O(h^5)\end{cases}

Consideriamo ora la combinazione lineare

-f(x_{i+2})+8f(x_{i+1})-8f(x_{i-1})+f(x_{i-2})

e sostituiamo gli sviluppi:

-f(x_{i+2})+8f(x_{i+1})-8f(x_{i-1})+f(x_{i-2

= -f(x_i) -f'(x_i)2h-2f''(x_i)h^2-4\frac{f''(x_i)}{3}h^3-2\frac{f''''(x_i)}{3}h^4+8f(x_i)+8f'(x_i)h+4f''(x_i)h^2+4\frac{f''(x_i)}{3}h^3+\frac{f''''(x_i)}{24}h^4-

-8f(x_i) +8f'(x_i)h-4f''(x_i)h^2+4\frac{f''(x_i)}{3}h^3-\frac{f''''(x_i)}{24}h^4+f(x_i)-f'(x_i)2h+2f''(x_i)h^2-4\frac{f''(x_i)}{3}h^3+2\frac{f''''(x_i)}{3}h^4+O(h^5)=12hf'(x_i)+O(h^5)

Da cui

f'(x_i)=\frac{-f(x_{i+2})+8f(x_{i+1})-8f(x_{i-1})+f(x_{i-2})}{12h}+O(h^4)=\frac{-f(x_i+2h)+8f(x_i+h)-8f(x_i-h)+f(x_i-2h)}{12h}+O(h^4)

(4)

Questa approssimazione della derivata prima ha un errore proporzionale a h⁴ ma coinvolge 4 punti.
In modo analogo si possono ricavare formule per approssimare le derivate superiori con errori proporzionali a h⁴.

Formula centrata della derivata seconda su 5 punti:

$f''(x_i)=\frac{-f(x_{i+2})+16f(x_{i+1})-30f(x_{i})+16f(x_{i-1})-f(x_{i-2})}{12h^2}+O(h^4)=\frac{-f(x_i+2h)+16f(x_i+h)-30f(x_{i})+16f(x_i-h)-f(x_i-2h)}{12h^2}+O(h^4)$ (5)

Formula centrata della derivata terza su 6 punti:

f'''(x_i)=\frac{-f(x_{i+3})+8f(x_{i+2})-13f(x_{i+1})+13f(x_{i-1})-8f(x_{i-2})+f(x_{i-3})}{8h^3}+O(h^4)

Formula centrata della derivata quarta su 7 punti:

$f''''(x_i)=\frac{-f(x_{i+3})+12f(x_{i+2})-39f(x_{i+1})+56f(x_i)-39f(x_{i-1})+12f(x_{i-2})-f(x_{i-3})}{6h^4}+O(h^4)$

L'ESTRAPOLAZIONE DI RICHARDSON

Le formule centrate delle derivate superiori sono via via sempre più complesse se si vuole calcolarle con maggiore precisione. Ma esiste una regola generale per costruire le formule centrate ?
Consideriamo di nuovo le espansioni di Taylor in avanti e indietro (1) e (2):

\begin{cases} f(x_{i+1})=f(x_i)+f'(x_i)h+\frac{f''(x_i)}{2}h^2+\frac{f'''(x_i)}{6}h^3+... \\ f(x_{i-1})=f(x_i) -f'(x_i)h+\frac{f''(x_i)}{2}h^2-\frac{f'''(x_i)}{6}h^3... \end{cases}

e la combinazione per ottenere la formula della first central approximation per la derivata prima:

\frac{f(x_{i+1})-f(x_{i-1})}{2h}=f'(x_i)+\frac{f'''(x_i)}{6}h^2+\frac{f^{V}(x_i)}{5!} h^4+...

Definiamo i rapporti incrementali in un certo x_i:

I_{1,1}(h)=\frac{f(x_{i+1})-f(x_{i-1})}{2h}=\frac{f(x_i+h)-f(x_i-h)}{2h}

I_{2,1}(h)=\frac{f\left(x_i+\frac{h}{2}\right)-f\left(x_i-\frac{h}{2}\right)}{2\cdot \left(\frac{h}{2}\right)}

E in generale: $I_{j,1}(h)=\frac{f\left(x_i+\frac{h}{2^{j-1}}\right)-f\left(x_i-\frac{h}{2^{j-1}}\right)}{2\cdot \left(\frac{h}{2^{j-1}}\right)}$			(6)
Questi rapporti incrementali possono, in generale, essere sviluppati in serie di Taylor nella forma: $I_{j,1}(h)=f'(x_i)+a_2\left(\frac{h}{2^{j-1}}\right)^2+a_4\left(\frac{h}{2^{j-1}}\right)^4+a_6\left(\frac{h}{2^{j-1}}\right)^6+...$			(7)

con a₂, a₄, a₆ dei coefficienti che dipendono dalle derivate dispari.
Consideriamo ora :

I_{1,1}(h)= f'(x_i)+a_2h^2+a_4h^4+...

I_{2,1}(h)= f'(x_i)+a_2 \frac{h^2}{4}+a_4 \frac{h^4}{16}+...

e l'espressione:

\frac{4I_{2,1}(h)-I_{1,1}(h)}{3}=\frac{4f'(x_i)+a_2h^2+a_4h^4/4+...-f'(x_i)-a_2h^2-a_4h^4-...}{3}=f'(x_i)-a_4\frac{h^4}{4}-...

Si ricava:

f'(x_i)=\frac{4I_{2,1}(h)-I_{1,1}(h)}{3}+O(h^4)

(8)

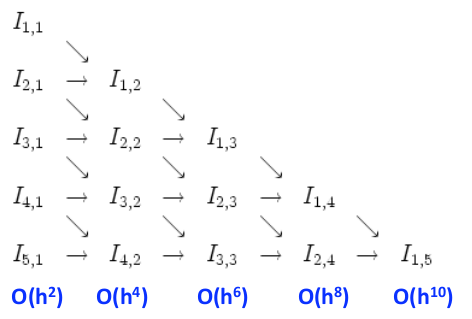
Si può osservare che, in questa forma, l'approssimazione della f'(x) ha di errore ridotto, di ordine O(h⁴) ( è una second approximation) ma qui abbiamo utilizzato una formula più semplice di quella ricavata prima per la derivata prima che coinvolgeva quattro punti .
Questo è un esempio di estrapolazione di Richardson che rappresenta un metodo in cui si combinano tra di loro due diverse stime numeriche per ottenere una più accurata, sfruttando la conoscenza dell'andamento dell'errore.

In generale definiamo i coefficienti:

I_{j,k}=\frac{4^{k-1}I_{j+1,k-1}-I_{j,k-1}}{4^{k-1}-1}

avendo precedentemente definito gli I_j,1 (nel caso della derivata vedi formula (7)).
In pratica gli I_j,1 rappresentano le approssimazioni con un maggiore livello di accuratezza secondo una potenza di 2 (calcolo della derivata prima centrata con un intervallo h a destra e a sinistra di x_i sempre più piccolo secondo potenze di 2)
Allora la grandezza L può essere approssimata dalla formula:

L=I_{j,k}+O(h^{2k})

Per esempio, nel caso della derivata prima, se k=1 e qualsiasi j abbiamo la formula (6) e (7):

I_{j,1}(h)=\frac{f\left(x_i+\frac{h}{2^{j-1}}\right)-f\left(x_i-\frac{h}{2^{j-1}}\right)}{2\cdot \left(\frac{h}{2^{j-1}}\right)}=f'(x_i)+a_2\left(\frac{h}{2^{j-1}}\right)^2+a_4\left(\frac{h}{2^{j-1}}\right)^4+a_6\left(\frac{h}{2^{j-1}}\right)^6+...

che approssima comunque f'(x_i) con un errore O(h²).
Ma con k=2 e j=1 si produce la formula (8):

f'(x_i)=I_{1,2}(h)=\frac{4I_{2,1}(h)-I_{1,1}(h)}{3}+O(h^4)

che approssima f'(x_i) con un errore O(h⁴).

In generale possiamo ottenere approssimazioni della derivata prima sempre più accurate seguendo lo schema di figura.
Per esempio per ottenere una approssimazione della derivata prima con un errore O(h⁶):

f'(x)=I_{1,3}+O(h^6)

dobbiamo calcolare I_1,3:

I_{1,3}=\frac{4^2I_{2,2}-I_{1,2}}{4^2-1}

Servono I_2,2 e I_1,2:

I_{2,2}=\frac{4^1I_{3,1}-I_{2,1}}{4^1-1}=\frac{4I_{3,1}-I_{2,1}}{3}\qquad I_{1,2}=\frac{4^1I_{2,1}-I_{1,1}}{4^1-1}=\frac{4I_{2,1}-I_{1,1}}{3}

Da cui:

I_{1,3}=\frac{16I_{2,2}-I_{1,2}}{15}=\frac{16\left(\frac{4I_{3,1}-I_{2,1}}{3}\right)-\left(\frac{4I_{2,1}-I_{1,1}}{3}\right)}{15}=\frac{64I_{3,1}-20I_{2,1}+I_{1,1}}{45}

Utilizzando la formula (6):

I_{3,1}=\frac{f\left(x_i+\frac{h}{4}\right)-f\left(x_i-\frac{h}{4}\right)}{\frac{h}{2}} \qquad I_{2,1}=\frac{f\left(x_i+\frac{h}{2}\right)-f\left(x_i-\frac{h}{2}\right)}{h}\qquad I_{1,1}=\frac{f(x_i+h)-f(x_i-h)}{2h}

Come ultimi esempi ricaviamo la second central approximation per la derivata prima e per la derivata seconda:

f'(x)=I_{1,2}+O(h^4)

Serve I_1,2 ma lo abbiamo già trovato:

I_{1,2}=\frac{4I_{2,1}-I_{1,1}}{3}=\frac{4\left(\frac{f\left(x_i+\frac{h}{2}\right)-f\left(x_i-\frac{h}{2}\right)}{h}\right)-\left(\frac{f\left(x_i+h\right)-f\left(x_i-h\right)}{2h}\right)}{3}= \frac{-f(x_i+h)+8f(x_i+h/2)-8f(x_i-h/2)+f(x_i-h)}{6h}

Questa espressione per la derivata prima sembra non uguale a quella della (3) perché il passo ha un diverso significato. In questa formula dal punto x_i lo spostamento è x_i±h/2 oppure x_i±h, in quella invece x_i±h oppure x_i+2h. Se si sostituisce h con 2h si ottiene la formula (3).

Derivata seconda:

f''(x)=I_{2,2}+O(h^4)

Serve I_2,2 ma lo abbiamo già trovato:

I_{2,2}=\frac{4^1I_{3,1}-I_{2,1}}{4^1-1}=\frac{4I_{3,1}-I_{2,1}}{3}

Ora bisogna definire, per la derivata seconda, i rapporti incrementali I_j,1.
Dalla formula (3) della first central approximation della derivata seconda:

f''(x_i)=\frac{f(x_{i+1})+f(x_{i-1})-2f(x_i)}{h^2}+O(h^2)

Si ha che :

I_{1,1}=\frac{f(x_i+h)+f(x_i-h)-2f(x_i)}{h^2}

Da cui, in generale, :

I_{j,1}=\frac{f\left(x_i+\frac{h}{2^{j-1}}\right)+f\left(x_i-\frac{h}{2^{j-1}}\right)-2f(x_i)}{\left(\frac{h}{2^{j-1}}\right)^2 }

I_2,1 :

I_{2,1}=\frac{f\left(x+h/2\right)+f\left(x-h/2\right)-2f(x_i)}{\frac{h^2}{4}}

I_3,1:

I_{3,1}=\frac{f\left(x+h/4\right)+f\left(x-h/4\right)-2f(x_i)}{\frac{h^2}{16}}

I_2,2:

I_{2,2}=\frac{4I_{3,1}-I_{2,1}}{3}=\frac{4\left[\frac{f\left(x+h/4\right)+f\left(x-h/4\right)-2f(x_i)}{\frac{h^2}{16}}\right]-\left[\frac{f\left(x+h/2\right)+f\left(x-h/2\right)-2f(x_i)}{\frac{h^2}{4}}\right]}{3}=

=\frac{64f(x+h/4)+64f(x-h/4)-128f(x)-4f(x+h/2)-4f(x-h/2)+8f(x)}{3h^2}=\frac{64f(x+h/4)+64f(x-h/4)-120f(x)-4f(x+h/2)-4f(x-h/2)}{3h^2}

Per confrontarla con la (5) sostituiamo h con 4h :

I_{2,2}=\frac{64f(x+h)+64f(x-h)-120f(x)-4f(x+2h)-4f(x-2h)}{48h^2}=\frac{16f(x+h)+16f(x-h)-30f(x)-f(x+2h)-f(x-2h)}{12h^2}

che è esattamente la (5)