Numerical Integration

INTEGRAZIONE NUMERICA

Il problema generale è calcolare l'integrale I :

I=\int_a^b f(x) \, dx

Questo problema è risolto dal Teorema Fondamentale del Calcolo Integrale:

Si cerca per via analitica la funzione F(x), detta funzione primitiva, tale che F'(x)= f(x)
Si calcola $I=\int_a^b f(x) \, dx= F(b)\,-\,F(a)$

Tuttavia accade che non si riesce a trovare per via analitica la primitiva o si possiede solo un insieme di valori della f(x) ottenuti sperimentalmente in corrispondenza di particolari valori della variabile indipendente x. In questi casi occorre utilizzare i metodi di integrazione numerica.
Una formula esplicita che permetta di approssimare l'integrale I viene detta formula di quadratura o formula d’integrazione numerica. La strategia generale è quella di sostituire alla funzione f(x) dei polinomi interpolatore di grado m su n+1 nodi distinti x_i che approssimano la f(x) tra questi nodi:

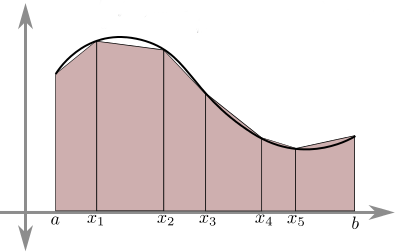
$f_m(x)=a_0 + a_1x^1+a_2x^2+a_3x^3+ ... + a_{m-1}x^{m-1}+a_mx^m$ Il calcolo dell'integrale diventa: $I=\int_a^b f(x) \, dx= \int_{a=x_0}^{x_1} f_{m1}(x) \, dx+\int_{x_1}^{x_2} f_{m2}(x) \, dx+\int_{x_2}^{x_3} f_{m3}(x) \, dx+...+\int_{x_{n-1}}^{b=x_n} f_{mn}(x) \, dx$
Le formule di quadratura che utilizzano polinomi interpolatori su nodi equispaziati si chiamano formule di Newton-Cotes.

POLINOMIO DI PRIMO ORDINE: REGOLA DEL TRAPEZOIDE
In questo caso, in ogni intervallo, il polinomio i-esimo è di primo ordine (un segmento di retta):

f_1(x)=a_0+a_1x

in generale è:

f_i(x)=f(x_{i-1})+\frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}}\cdot (x-x_{i-1})

che è l'equazione della retta passante per due nodi [x_i-1,f(x_i-1)] e [x_i,f(x_i)].

Poiché i nodi sono equispaziati calcoliamo la loro (costante) distanza reciproca e la chiamiamo

h= \frac{b-a}{n}

Sostituendo nell' i-esimo integrale:

\int_{x_{i-1}}^{x_i} f_i(x) \,dx=\int_{x_{i-1}}^{x_i} \left[f(x_{i-1})+\frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}}\cdot (x-x_{i-1})\right]\,dx=f(x_{i-1})\,h+\frac{f(x_i)-f(x_{i-1})}{h}\frac{h²}{2}=\frac{f(x_{i-1})}{2}\,h+\frac{f(x_i)}{2}\,h

E il calcolo dell'integrale diventa:

I=\left[\frac{f(a)}{2}+\frac{f(x_1)}{2}+\frac{f(x_1)}{2}+\frac{f(x_2)}{2}+ \frac{f(x_2)}{2}+\frac{f(x_3)}{2}....\frac{f(x_{n-1})}{2}+\frac{f(b)}{2}\right] \cdot h=\frac{h}{2}\left[f(a)+2 \sum_{i=1}^{n-1}f(x_i) +f(b)\right]=

=(b-a)\frac{f(a)+2 \sum_{i=1}^{n-1}f(a+ih) +f(b)}{2n

Che è in definitiva la somma dell'area di n trapezi rettangoli.
L'errore totale nell'i-esimo integrale si può stimare con la formula:

E_i= -\frac{1}{12}f''(ξ)h^3

con ξ un punto tra x_i-1 e x_i. Si può osservare che l'errore cresce con il cubo dell'ampiezza dell'intervallo.
L'errore totale è:

E_t = -\frac{1}{12}\frac{(b-a)^3}{n^3}\sum_{i=1}^nf''(ξ_i)=-\frac{1}{12}\frac{\left(b-a\right)^3}{n^2}\frac{\sum_{i=1}^nf''(ξ_i)}{n}=-\frac{1}{12}\frac{\left(b-a\right)^3}{n^2}<f''>=-\frac{h^2}{12}\left(b-a\right)<f''>

con <f''> il valore medio della derivata seconda.
Si può osservare che, poiché l'errore è proporzionale a h², dimezzando l'ampiezza degli intervalli l'errore si riduce di un fattore 4 (ma ad un certo punto bisogna limitarsi a causa dell'errore di arrotondamento).

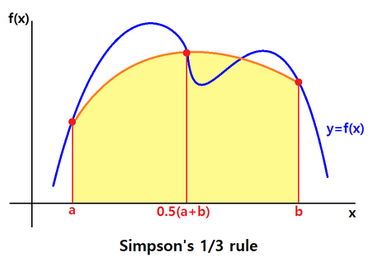
POLINOMIO DI SECONDO ORDINE: REGOLA DI SIMPSON 1/3
La successiva approssimazione è considerare in ogni intervallo un polinomio interpolante al secondo ordine (parabola):

f_2(x)=a_0+a_1x+a_2x^2

Tuttavia per definire una parabola sono necessari almeno tre punti. La più semplice scelta è considerare gli estremi dell'intervallo e il punto medio e poiché i nodi si suppongono equispaziati basta considerare tre punti consecutivi x_i , x_i + h e x_i + 2h. Quindi, dati i tre punti, occorre ricavare i coefficienti a₀, a₁, a₂ e poi calcolare l'integrale tra x_i e x_i + 2h. Il risultato è:

I_i= \frac{h}{3}\left[f(x_i ) + 4f(x_i+h) + f(x_i+2h)\right]

con

h={x_{i+1}-x_i}

. A causa del fattore 1/3 questa formula è detta Regola di Simpson 1/3. L'errore è

E=-\frac{h^5}{90}f^{IV}(ξ)

In generale, se consideriamo un intero intervallo [a,b] con n nodi il calcolo dell'integrale diventa:

I=\left(b-a\right)\cdot \frac{f(a)+4\sum_{i=1,3,5}^{n-1}f(a+ih)+2\sum_{i=2,4,6}^{n-2}f(a+ih)+f(b)}{3n

con

h=\frac{b-a}{n}

. Per ogni tre punti passa una diversa parabola interpolatrice.
L'errore totale è :

E_t≃-\frac{\left(b-a\right)^5}{180n^4}<f^{IV}>=-\frac{h^4}{180}\left(b-a\right)<f^{IV}>

con <f^IV> il valore medio della derivata quarta nell'intervallo [a,b].
Poiché l'errore è proporzionale a h⁴ dimezzando l'ampiezza degli intervalli l'errore totale si riduce di un fattore 16

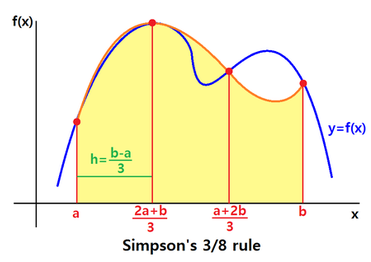
POLINOMIO DI TERZO ORDINE: REGOLA DI SIMPSON 3/8
In questo caso, in ogni intervallo, il polinomio è al terzo ordine (una cubica):

f_3(x)=a_0+a_1x+a_2x^2+a_3a^3

Per definire una cubica servono quattro punti. In modo analogo per la Regola 1/3 si scelgono punti equispaziati (quattro): a= x_i, (2a+b)/3= x_i + h, (a+2b)/3= x_i + 2h, b= x_i + 3h. Poi, dati i quattro punti, occorre ricavare i coefficienti a₀, a₁, a₂ e a₄ e infine calcolare l'integrale tra a e b. Il risultato è:

I=\frac{3h}{8}\left[f(a)+3f(a+h)+3f(a+2h)+f(b)\right]

con

h=\frac{b-a}{3}

. A causa del fattore 3/8 questa formula è detta Regola di Simpson 3/8.
In generale, se consideriamo un intero intervallo [a,b] con n nodi il calcolo dell'integrale diventa:

I=3\left(b-a\right)\frac{f(a)+3 \sum_{i=1,4,7}^{n-2}f(a+ih) +3\sum_{i=2,5,8}^{n-1}f(a+ih) +2\sum_{3,6,9}^{n-3}f(a+ih)+f(b)}{8n}

con

h=\frac{b-a}{n}

. Per ogni quattro punti passa una cubica interpolatrice.

L'errore totale è :

E_t=-\frac{h^4}{80}\left(b-a\right)<f^{IV}>

con <f^IV> il valore medio della derivata quarta nell'intervallo [a,b].
Poiché l'errore è proporzionale a h⁴ dimezzando l'ampiezza degli intervalli l'errore totale si riduce di un fattore 16

L'ESTRAPOLAZIONE DI RICHARDSON
L'estrapolazione di Richardson rappresenta un metodo in cui si combinano tra di loro due diverse stime numeriche dell'integrale per ottenerne una più accurata, sfruttando la conoscenza dell'andamento dell'errore.
Supponiamo di aver applicato un dato metodo per stimare un'integrale e abbiamo ottenuto due stime dell'integrale con due spaziature diverse, h₁ e h₂. Deve essere:

I=I(h_1) + E(h_1)=I(h_2)+E(h_2)

con I(h) la stima dell'integrale e E(h) il suo errore di troncamento.
Se abbiamo usato il metodo del trapezoide i due errori saranno del tipo :

E(h)=-\frac{h^2}{12}\left(b-a\right)<f''>

, supponendo indipendente da h il valore medio di f'' e poichè l'intervallo è lo stesso si ha:

\frac{E(h_1)}{E(h_2)}=\frac{h_1^2}{h_2^2}⇒ E(h_1)=E(h_2)\,\frac{h_1^2}{h_2^2}

sostituendo l'errore del primo integrale e uguagliando i due integrali:

I(h_1)+E(h_2)\,\left(\frac{h_1}{h_2}\right)^2=I(h_2)+E(h_2)

si può ricavare :

E(h_2)=\frac{I(h_1)-I(h_2)}{1-\left(h_1/h_2\right)^2}

Abbiamo così ottenuto una stima dell'errore del secondo integrale che possiamo scrivere:

I=I(h_2)+E(h_2)≃I(h_2)+\frac{I(h_1)-I(h_2)}{1-\left(h_1/h_2\right)^2}

Avendo una stima dell'errore sul secondo integrale possiamo migliorare la sua approssimazione.
Per esempio se scegliamo h₂= h₁/2 la stima dell'integrale diventa:

I≃I(h_2)+\frac{I(h_2)-I(h_1)}{2^2-1}=\frac{4^1I(h_2)-I(h_1)}{4^1-1}=\frac{4I(h_2)-I(h_1)}{3}

(1)

stima migliore di I(h₂) perchè la nuova stima ha un errore minore, dell'ordine di O(h⁴).
Il metodo può essere ulteriormente iterato. Se si sono ottenute due diverse stime con accuratezza O(h⁴) ottenute con h₂= h₁/2 queste possono essere combinate per ottenere una nuova stima che avrà accuratezza O(h⁶):

I≃I(h_2)+\frac{I(h_1)-I(h_2)}{1-(h_1/h_2)^4}=I(h_2)-\frac{I(h_2)-I(h_1)}{2^4-1}=\frac{2^4I(h_2)-I(h_1)}{2^4-1}=\frac{4^2I(h_2)-I(h_1)}{4^2-1}=\frac{16I(h_2)-I(h_1)}{15}

Questo è un esempio di estrapolazione di Richardson che rappresenta un metodo in cui si combinano tra di loro due diverse stime numeriche per ottenere una più accurata, sfruttando la conoscenza dell'andamento dell'errore.
L'algoritmo di integrazione di Romberg corrisponde all'implementazione numerica del metodo di estrapolazione di Richardson utilizzando sempre h₂= h₁/2. In generale i coefficienti necessari per generare le diverse stime possono essere scritti come:

I_{j,k}=\frac{4^{k-1}I_{j+1,k-1}-I_{j,k-1}}{4^{k-1}-1}

k rappresenta l'ordine di accuratezza: con k=1 otteniamo una stima con errore O(h²), con k=2 otteniamo una stima con errore O(h⁴), con k=3 otteniamo una stima con errore O(h⁶) ecc..
j rappresenta il livello di accuratezza: j+1 è più accurato di j

Per esempio consideriamo la stima (1). Dobbiamo calcolare I_1,2 , per farlo utilizziamo le stime I_1,1 e I_2,1.
I_2,1 ha un livello di accuratezza superiore di I_1,1 perchè h₂= h₁/2. Tutte e due hanno lo stesso ordine di accuratezza perchè k=1.

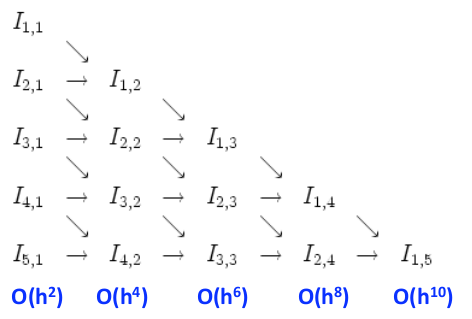Per ottenere la stima I_1,3 occorre possedere le stime I_1,2 e I_2,2. Questa volta l'ordine di accuratezza è O(h⁴) per tutte e due le stime ma I_2,2 deve essere stata stimata con un intervallo pari alla metà dell'intervallo con cui è stata stimata I_1,2: deve possedere un livello di accuratezza superiore.

LA QUADRATURA DI GAUSS
Nelle formule di Newton-Cotes l'integrazione numerica della funzione è sviluppata secondo punti predeterminati dall'ampiezza scelta h. Ma questo metodo non offre buoni risultati se la funzione non è regolare.

Nella quadratura di Gauss, in un determinato intervallo, l'approssimazione dell'integrale può essere migliorata usando due punti interni indeterminati scelti in modo da minimizzare l'errore di integrazione.
Per esempio, in un determinato intervallo la formula del trapezoide è:

I≃\left(b-a\right)\frac{f(a)+f(b)}{2}=\frac{b-a}{2}f(a)+\frac{b-a}{2}f(b)

ma a e b non sono noti si può comunque scrivere:

I≃c_0f(x_0) + c_1f(x_1)

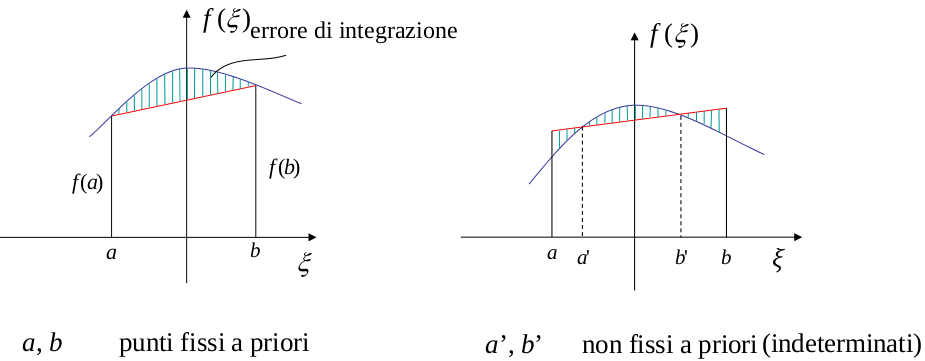dove x₀ e x₁ sono due punti non noti interni all'intervallo di integrazione e c₀ e c₁ sono opportuni coefficienti da determinarsi.
Per determinare questi due punti supponiamo che l'integrale della funzione dia un risultato esatto integrando analiticamente una funzione polinomiale del terzo ordine:

f(x)= a_0 + a_1x+a_2x^2+a_3x^3

L'integrale esatto è:

I=\int_a^b {\left(a_0 + a_1x+a_2x^2+a_3x^3\right)}\,dx=a_0\left(b-a\right)+a_1\frac{b^2-a^2}{2}+a_2\frac{b^3-a^3}{3}+a_4\frac{b^4-a^4}{4}

L'integrale approssimato è:

I=c_0f(x_0)+c_1f(x_1)=c_0\left(a_0+a_1x_0+a_2x_0^2+a_3x_0^3\right)+ c_1\left(a_0+a_1x_1+a_2x_1^2+a_3x_1^3\right)=

= \left(c_0+c_1\right)a_0+\left(c_0x_0+c_1x_1\right)a_1+(c_0x_0^2+c_1x_1^2)a_2+(c_0x_0^3+c_1x_1^3)a_3

dal confronto dei due integrali derivano le condizioni:

\begin{cases} c_0+c_1=b-a\\ c_0x_0+c_1x_1=\frac{b^2-a^2}{2}\\c_0x_0^2+c_1x_1^2=\frac{b^3-a^3}{3}\\ c_0x_0^3+c_1x_1^3=\frac{b^4-a^4}{4} \end{cases}

Per risolvere il sistema si può fare un cambio di variabile in modo che a=-1 e b= 1. Il sistema diventa:

\begin{cases} c_0+c_1=b-a=1-(-1)=2\\ c_0x_0+c_1x_1=\frac{b^2-a^2}{2}=\frac{1-1}{2}=0\\c_0x_0^2+c_1x_1^2=\frac{b^3-a^3}{3}=\frac{1-\left(-1\right)}{3}=\frac{2}{3}\\ c_0x_0^3+c_1x_1^3=\frac{b^4-a^4}{4} =\frac{1-1}{4}=0\end{cases}

Risolvendo si ha:

\begin{cases} c_0=1 \\ c_1=1\\ x_0=-\frac{1}{\sqrt{3}} \\ x_1=\frac{1}{\sqrt{3}} \end{cases}

. Pertanto

I=f\left(-\frac{1}{\sqrt{3}}\right)+f\left(\frac{1}{\sqrt{3}}\right)

è la formula a due punti di Gauss-Legendre.
Per tornare ai limiti di integrazione a e b è necessario fare il seguente cambio di variabile:

x= k_0+k_1\widebar{x}

I limiti di integrazione sono:

\begin{cases} x=a⇒\widebar{x}=-1⇒ a=k_0+k_1\left(-1\right)\\ x=b⇒\widebar{x}=+1⇒ a=k_0+k_1\left(+1\right) \end{cases}

Le soluzioni sono:

k_0=\frac{b+a}{2}\;

k_1=\frac{b-a}{2}

da cui

x=\frac{\left(b+a\right)+\left(b-a\right)\widebar{x}}{2}⇒\begin{cases} x_0=\frac{\left(b+a\right)}{2}-\frac{1}{\sqrt{3}}\frac{b-a}{2} \\ x_1=\frac{\left(b+a\right)}{2}+\frac{1}{\sqrt{3}}\frac{b-a}{2} \\c_0=c_1=\frac{\left(b-a\right)}{2}\end{cases}

e l'integrale è:

I=c_0f(x_0)+c_1f(x_1)=\frac{b-a}{2}f\left(\frac{b+a}{2}-\frac{1}{\sqrt{3}}\frac{b-a}{2}\right)+\frac{b-a}{2}f\left(\frac{b+a}{2}+\frac{1}{\sqrt{3}}\frac{b-a}{2}\right)

In maniera analoga si possono sviluppare versioni di quadratura di Gauss-Legendre agli ordini superiori.
Si può fare di meglio utilizzando tre punti interni all'intervallo.
Si ha:

I≃\int_a^b f(x)\,dx = c_0f(x_0)+c_1f(x_1)+c_2f(x_2)

I coefficienti c₀, c₁, c₂ e le ascisse x₀, x₁, x₂ sono calcolati assumendo che l'integrale è esattamente calcolato utilizzando il polinomio di quinto grado (occorrono sei equazioni lineari):

f(x)= a_0 + a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5

e in questo caso, ponendo i limiti di integrazione a=-1 e b= 1, si ottiene:

\quad \begin{cases} c_0=\frac{5}{9} \\ c_1=\frac{8}{9} \\c_2=\frac{5 }{9}\end{cases} \qquad \begin{cases} x_0=-\frac{232379}{300000}≃-0.7746 \\ x_1=0 \\x_2=\frac{232379}{300000}≃0.7746\end{cases}