CONICHE: DALLA FORMA GENERALE ALLA FORMA CANONICA

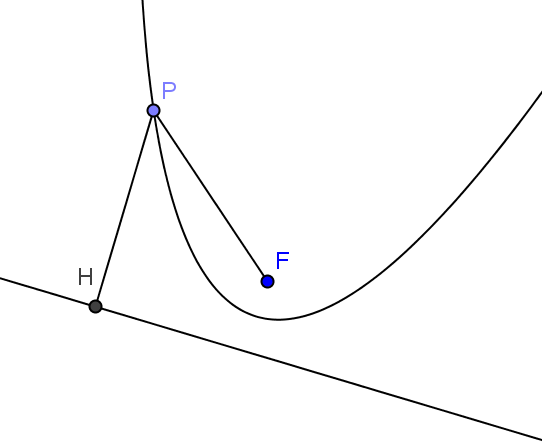
Una "conica" è il luogo geometrico dei punti P per i quali, dati una retta d (direttrice) e un punto F esterno ad essa, è costante il rapporto tra le distanze di P da F e di P da d.


Se la direttrice d ha equazione px + qy + s = 0, il fuoco è il puntoF(α,β) e il punto P è P(x,y), una conica ha equazione: $\bar{PF} = e \cdot \bar{PH} \to \sqrt{{(x - α)}^{2} + {(y - β)}^{2}} = e \cdot \frac{∣ px + qy + s ∣}{\sqrt{p^{2} + q^{2}}}$ La costante di proporzionalità è detta eccentricità. Sviluppando algebricamente si ottiene:

$(p^{2} + q^{2} - e^{2} p^{2}) \cdot x^{2} + (p^{2} + q^{2} - e^{2} q^{2}) \cdot y^{2} - 2 e^{2} p \cdot q \cdot xy - 2 [α (p^{2} + q^{2}) + e^{2} p \cdot s] \cdot x - 2 [β (p^{2} + q^{2}) + e^{2} q \cdot s] \cdot y + (p^{2} + q^{2}) (α^{2} + β^{2}) - e^{2} s^{2} = 0$

Posto ora:


$a = p^{2} + q^{2} - e^{2} p^{2}$	$b = - e^{2} \cdot p \cdot q$	$c = p^{2} + q^{2} - e^{2} q^{2}$
$d = - [α (p^{2} + q^{2}) + e^{2} \cdot p \cdot s]$	$e = - [β (p^{2} + q^{2}) + e^{2} \cdot q \cdot s]$	$f = (p^{2} + q^{2}) (α^{2} + β^{2}) - e^{2} \cdot s^{2}$

Si può scrivere:

$a \cdot x^{2} + 2 b \cdot xy + c \cdot y^{2} + 2 d \cdot x + 2 e \cdot y + f = 0$

che è l'equazione generale di una conica.

Occorre ora calcolare due parametri.

Un determinante: $Δ = ∣ \begin{matrix} a & b & d \\ b & c & e \\ d & e & f \end{matrix} ∣$
Un determinante : $δ = ∣ \begin{matrix} a & b \\ b & c \end{matrix} ∣$

Si può dimostrare che:

Se Δ = 0, la conica rappresenta l'unione di due rette, o una retta solo, o un punto, o un luogo vuoto
Se Δ≠ 0, bisogna distinguere i casi:
- se δ = 0 la conica è una parabola (e=1)
- se δ < 0 la conica è una iperbole (e > 1)
- se δ > 0
- la conica è una ellisse (e < 1) se il segno di a e c è opposto a quello di Δ
- la conica è un luogo vuoto se il segno di a e c è quello di Δ

Per ridurre una conica dalla forma generale alla forma canonica bisogna effettuare una isometria. Il metodo è:

Riconoscere la conica (calcola il δ)
Trovare il centro di simmetria C(h,k) della conica dato dall'intersezione delle rette : ${\begin{matrix} t : a \cdot x + b \cdot y + d = 0 \\ v : c \cdot y + b \cdot x + e = 0 \end{matrix}$
Traslare la conica di un vettore V(-h, -k) in modo da portare il centro di simmetria sull'origine degli assi
Ruotare la conica di un angolo che verifica l'equazione $b \cdot \tan^{2} φ - (c - a) \cdot \tan φ - b = 0$ (rotazione necessaria solo se presente il termine misto xy)
Se la tangente è positiva ruotare in senso orario (rotazione inversa), se la tangente è negativa ruotare in senso antiorario (rotazione diretta).

Nel caso della parabola non esiste centro di simmetria e le rette t e v sono parallele. Ciò si riconosce calcolando il determinante δ dei coefficienti delle incognite che in questo caso è uguale a zero. Bisogna solo ruotare la conica.