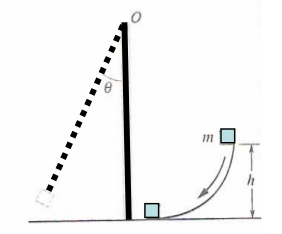
La particella di massa m in figura scende, scivolando da un altezza h= 2.5 m, una superficie priva di;attrito andando ad urtarne l'estremità dell'asta verticale omogenea (massa M= 3m, lunghezza d= 1 m), alla quale si appiccica. L'asta, libera di ruotare, senza attrito apprezzabile, intorno alla propria estremità (punto O), si arresta all'angolo θ rispetto alla verticale. Si calcoli θ in termini dei parametri dati.

La particella urta l'estremità dell'asta con una velocità che si può calcolare applicando il principio di conservazione dell'energia meccanica: $$\mathit{mgh}=\frac{1}{2}m{v}^2\to v=\sqrt{2gh}$$ L'urto è completamente anelastico, avviene in tempi piccoli e si può applicare la conservazione del momento angolare rispetto il punto O: $$L_i=L_f\to mvd=(m{d}^2+I_O)\omega$$ Il momento d'inerzia dell'asta rispetto al punto O è M d²/3, da cui, sostituendo troviamo la velocità angolare: $$mvd=(m{d}^2+I_O)\omega \to mvd=(m{d}^2+\frac{1}{3}M{d}^2)\omega \to mvd=(m{d}^2+\frac{1}{3}3m{d}^2)\omega \to vd=(d^2+d^2)\omega \to \omega =\frac{v}{2d}$$ Per finire riapplichiamo il principio di conservazione dell'energia meccanica:

$$K_i=U_f\to \frac{1}{2}I{\omega }^2=(m+M){\mathit{gh}}_f\to \frac{1}{2}\cdot 2m{d}^2\frac{v^2}{4d^2}=(m+3m){\mathit{gh}}_f\to \frac{v^2}{4}=4g{h}_f\to h_f=\frac{v^2}{16g}$$ Inseriamo la velocità prima dell'urto: $$h_f=\frac{v^2}{16g}=\frac{2gh}{16g}=\frac{h}{8}$$ Ma mentre prima h era l'altezza della particella ora h_f è l'altezza del centro di massa. Per conoscere l'angolo θ occorre conoscere la posizione del centro di massa ripetto al punto O.
Dalla sua definizione: $$y_{\mathit{cm}}=\frac{m{y}_1+M{y}_2}{m+M}=\frac{md+M\frac{d}{2}}{m+M}=\frac{md+3m\frac{d}{2}}{m+3m}=\frac{5}{8}d$$ L'angolo θ è dato da: $$\theta =\arccos \left(\frac{\frac{5}{8}d-h_f}{\frac{5}{8}d}\right)=\arccos \left(\frac{\frac{5}{8}d-h/8}{\frac{5}{8}d}\right)=\arccos \left(\frac{\frac{5}{8}-\frac{2.5}{8}}{\frac{5}{8}}\right)=\arccos \left(\frac{2.5}{5}\right)=60°$$