Paraxial Approximation

L'APPROSSIMAZIONE PARASSIALE NEGLI SPECCHI

LO SPECCHIO PARABOLICO E IPERBOLICO

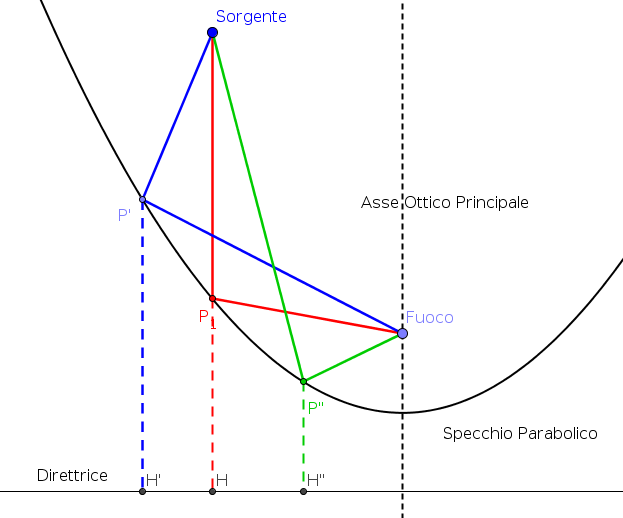
Supponiamo che tre raggi sono emessi dalla sorgente S, che raggiungano lo specchio parabolico e che, riflessi, passino per il fuoco. Solo la riflessione del raggio che incide in P è fisicamente possibile. Infatti, per le proprietà della parabola sono uguali le distanze:

\begin{cases} \widebar{P'H'}=\widebar{P'F} \\ \widebar{PH}=\widebar{PF}\\ \widebar{P''H''}=\widebar{P''F} \end{cases}

I cammini ottici sono

\begin{cases} L_1=\widebar{P'F}+\widebar{SP'} = \widebar{P'H'}+\widebar{SP'}\\ L_2=\widebar{PF}+\widebar{SP}=\widebar{PH}+\widebar{SP}\\ L_3= \widebar{P''F}+\widebar{SP''} =\widebar{P''H''}+\widebar{SP''}\end{cases}

La distanza più piccola tra un punto e una retta è lungo la perpendicolare per quel punto. Allora L₁ è il minimo cammino ottico ed è l'unico possibile per il Principio di Fermat.

"Tutti i raggi paralleli all'asse ottico principale, quando riflessi da uno specchio parabolico, passano per il fuoco"

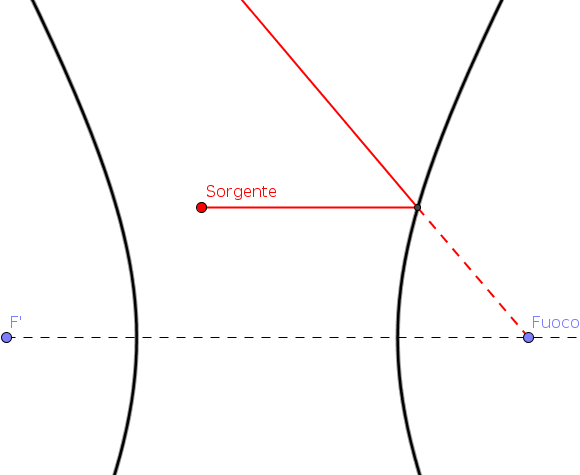
È possibile ache produrre uno specchio iperbolico ma in quel caso:

"I prolungamenti di tutti i raggi paralleli all'asse ottico principale, quando riflessi da uno specchio iperbolico, passano per il fuoco"

Il fuoco di uno specchio iperbolico è virtuale, quello di uno specchio parabolico è reale.

SPECCHI SFERICI E SPECCHI PARABOLICI

La superficie di uno specchio sferico è quella di una calotta sferica. Sotto certe approssimazioni uno specchio sferico, di raggio doppio della distanza focale, può approssimare uno specchio parabolico.

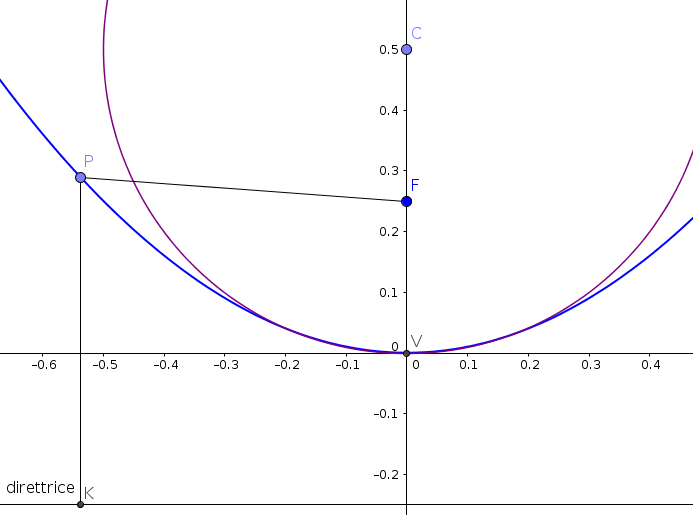
Una circonferenza con centro nell'asse delle ordinate è descritta dalla funzione: $y(x)=R±\sqrt{R^2-x^2}$ La semicirconferenza passante per l'origine dalla funzione: $y(x)=R-\sqrt{R^2-x^2}$ Sviluppiamo in serie di Taylor la funzione nell'intorno dell'origine (è una funzione pari e quindi lo sviluppo presenterà solo termini pari): $y(x)=y(0)+\frac{y''(0)}{2!}x^2+\frac{y''''(0)}{4!}x^4+...$ Le derivate: $y'(x)=-\frac{1}{2\sqrt{R^2-x^2}}\cdot \left(-2x\right)=\frac{x}{\sqrt{R^2-x^2}}$ $y''(x)=\frac{1}{\sqrt{R^2-x^2}}+x\left[-\frac{1}{2}\cdot \frac{-2x}{\sqrt{\left(R^2-x^2\right)^3}}\right]=\frac{R^2-x^2+x^2}{\sqrt{(R^2-x^2)^3}}=\frac{R^2}{\sqrt{(R^2-x^2)^3}}$ $y'''(x)=R^2\left(-\frac{3}{2}\right)(R^2-x^2)^{-3/2-1}\cdot(-2x)=\frac{3R^2x}{\sqrt{(R^2-x^2)^5}}$
$y''''(x)=3R^2\left[\frac{1}{\sqrt{(R^2-x^2)^5}}-\frac{5x}{2}(R^2-x^2)^{-5/2-1}\cdot (-2x)\right]=3R^2\left(\frac{1}{\sqrt{(R^2-x^2)^5}}+\frac{5x^2}{\sqrt{(R^2-x^2)^7}}\right)$ In x=0: $\begin{cases} y(0)=0 \\ y''(0)=\frac{1}{R}\\y''''(0)=\frac{3}{R^3} \end{cases}$ Sostituendo nello sviluppo: $y(x)=0+\frac{1}{R}\frac{x^2}{2}+\frac{3}{R^3}\frac{x^4}{24}+...=\frac{x^2}{2R}+\frac{1}{8}\frac{x^4}{R^3}+...$ L'equazione di una parabola con vertice nell'origine è: $y(x)=\frac{x^2}{4f}$ con f ordinata del fuoco. Quindi se R= 2f e se $\frac{x^2}{2R}≫\frac{x^4}{8R^3}⇒x^2≪4R^2⇒x≪2R$ allora è possibile sostituire uno specchio parabolico con uno specchio sferico.
L'EQUAZIONE DEI PUNTI CONIUGATI

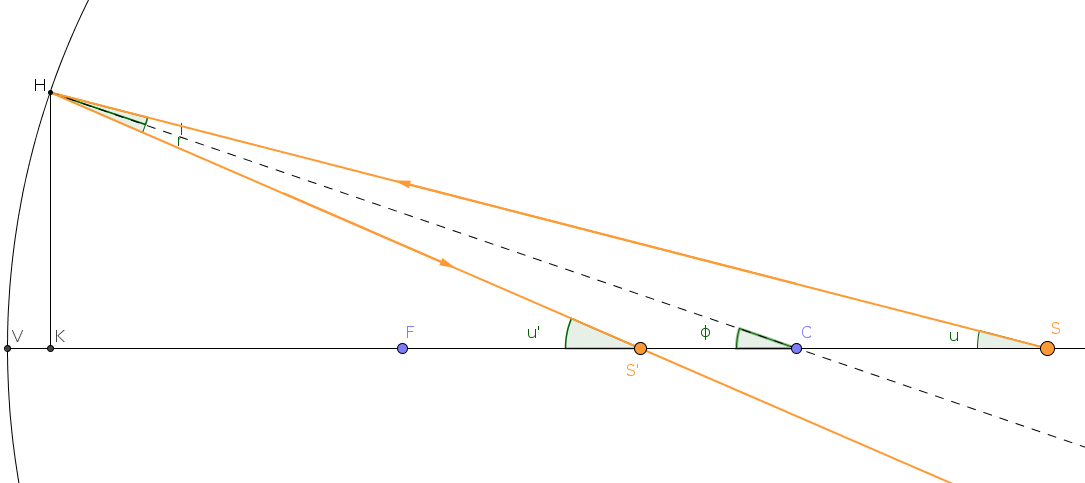
S è una sorgente e S' è la sua immagine. Dalla figura (Teorema angolo esterno) : $u'=ϕ+r$ e $ϕ=i+u$ Ma i = r, da cui: $u+u'=ϕ+r+ϕ-i=2ϕ$ Definizione tangente: $\begin{cases} \tan\left({u}\right)=\frac{\widebar{HK}}{\widebar{KS}} \\ \tan\left({u'}\right)=\frac{\widebar{HK}}{\widebar{KS'}}\\\tan\left({ϕ}\right)=\frac{\widebar{\widebar{HK}}}{\widebar{KC}} \end{case$
In approssimazione parassiale : $\begin{cases} \widebar{KS}≃\widebar{VS}=p \\ \widebar{KS'}≃\widebar{VS'}=q\\\widebar{KC}≃\widebar{VC}=R \end{cases} \qquad \begin{cases}\tan\left({u}\right)≃u \\\tan\left({u'}\right)≃u'\\\tan\left({ϕ}\right)≃ϕ \end{cases}$ Da cui, sostituendo: $\frac{\widebar{HK}}{p}+\frac{\widebar{HK}}{q}=2\frac{\widebar{HK}}{R}$ l'equazione dei punti coniugati: $\frac{1}{p}+\frac{1}{q}=\frac{1}{f}$ con f= R/2
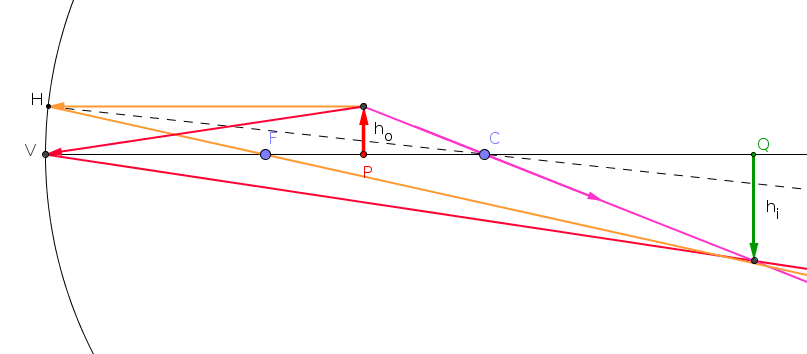
In approssimazione parassiale inoltre si ha che: $\begin{cases} h_o=\widehat{i }\cdot p \\ h_i = \widehat{r} \cdot q \end{cases}$ Definiamo ingrandimento lineare G: $G= \frac{h_i}{h_o}$ e lo vogliamo negativo se l'immagine è capovolta e positivo se è diritta. Allora, in approssimazione parassiale,: $G= -\frac{q}{p}$
Formazione dell'immagine senza l'approssimazione parassiale.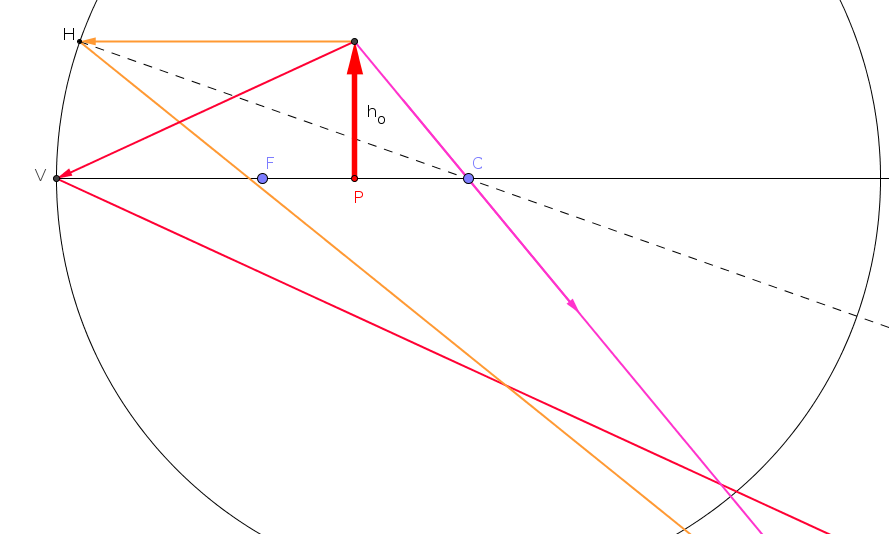