IL TEOREMA DEL GUSCIO SFERICO

Due masse, una puntiforme e l'altra un guscio sferico, interagiscono gravitazionalmente. Per l'anello colorato di massa dm di figura la forza generata sulla massa M è diretta lungo OA ed è uguale a:

$dF = G \cdot \frac{M \cdot dm}{x^{2}} \cdot \cos α$

Se il guscio sferico è omogeneo di densità ρ la massa dell'anello dm è:

$dm = ρ \cdot dV = ρ \cdot 2 πR \sin θ \cdot Rdθ$ ·s

con s lo spessore del guscio sferico.

Quindi la forza è:

$dF = GM \cdot 2 π R^{2} sρ \cdot \frac{\cos α \cdot \sin θ}{x^{2}} \cdot dθ$

Esprimiamo la forza tra anello e massa M in funzione solo di x .

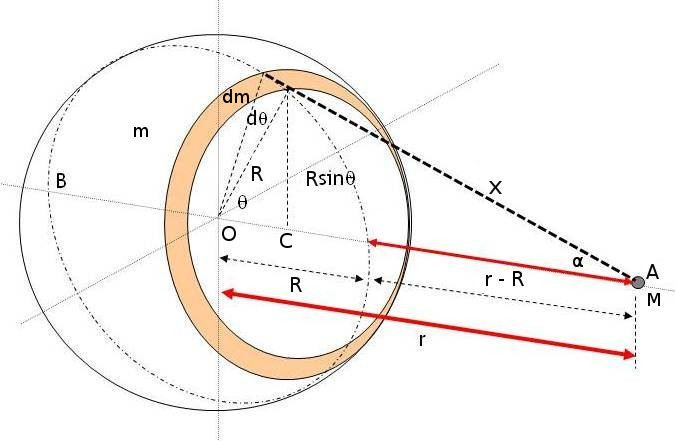
Applicando il teorema del coseno di Carnot:

$x^{2} = R^{2} + r^{2} - 2 Rr \cdot \cos θ \Rightarrow R \cos θ = \frac{r^{2} + R^{2} - x^{2}}{2 r}$

Dalla figura si può osservare che :

$\cos α = \frac{\bar{AC}}{x} = \frac{\bar{AO} - \bar{OC}}{x} = \frac{r - R \cos θ}{x} = \frac{r - \frac{r^{2} + R^{2} - x^{2}}{2 r}}{x} = \frac{2 r^{2} - r^{2} - R^{2} + x^{2}}{2 r x} = \frac{r^{2} - R^{2} + x^{2}}{2 r x}$

Infine differenziando Rcosθ:

$\frac{ⅆ (R \cos θ)}{ⅆ θ} = \frac{d}{dx} (\frac{r^{2} + R^{2}}{2 r} - \frac{x^{2}}{2 r}) \Rightarrow - R \cdot \sin θ \cdot dθ = - \frac{x}{r} \cdot dx \Rightarrow \sin θd θ = \frac{x}{rR} \cdot dx$

Sostituendo tutto nella forza dF:

$dF = GM \cdot 2 π R^{2} sρ \cdot \frac{r^{2} - R^{2} + x^{2}}{2 r x^{3}} \cdot \frac{x}{rR} \cdot dx = \frac{GMπRsρ}{r^{2}} \cdot \frac{r^{2} - R^{2} + x^{2}}{x^{2}} \cdot dx$

Integrando da r-R a r+R:

$F = \frac{GMπRsρ}{r^{2}} \cdot \int_{r - R}^{r + R} \frac{r^{2} - R^{2} + x^{2}}{x^{2}} dx = \frac{GMπRsρ}{r^{2}} \cdot [(r^{2} - R^{2}) \int_{r - R}^{r + R} \frac{1}{x^{2}} dx + \int_{r - R}^{r + R} dx] = \frac{GMπRsρ}{r^{2}} [(r^{2} - R^{2}) (- \frac{1}{r + R} + \frac{1}{r - R}) + (r + R - r + R)] =$

$= \frac{GMπRsρ}{r^{2}} \cdot [(r^{2} - R^{2}) (\frac{R - r + r + R}{r^{2} - R^{2}}) + 2 R] = \frac{GMπRsρ}{r^{2}} \cdot 4 R = \frac{GM}{r^{2}} \cdot ρ \cdot s \cdot 4 π R^{2} = \frac{GMm}{r^{2}}$

(il volume del guscio sferico è 4πR²·s).

Si è così dimostrato che l'interazione tra un guscio sferico di massa m e una massa puntiforme di massa M è equivalente all'interazione di due masse puntiformi di massa M ed m con la massa m collocata al centro del guscio sferico