ABERRAZIONI OTTICHE

LE ABERRAZIONI

Un sistema ottico ideale mostra sorgenti puntiformi nel suo piano focale come immagini puntiformi sia nella zona centrale, sia nella periferia. In ottica parassiale lenti o specchi formano di una sorgente puntiforme una immagine puntiforme ma l'approssimazione è valida finchè lo spessore delle lenti o l'apertura degli specchi sono piccole rispetto le altre distanze, se i raggi sono parassiali e se la radiazione è monocromatica. Nella relatà queste condizioni non sempre sono rispettate e, di conseguenza, l'immagine formata dai sistemi ottici è condizionata da vari tipi di distorsioni che sono chiamate aberrazioni ottiche. In presenza di abberrazioni le immagini di sorgenti puntiformi hanno la tendenza a divenire delle macchie più o meno distribuite a seconda della configurazione ottica, del tipo di lavorazione delle ottiche ed a seconda della posizione sul piano focale. Esistono cinque tipi di aberrazioni geometriche : aberrazione sferica; astigmatismo; coma; curvatura di campo; distorsione. In più, se la radiazione non è monocromatica, e solo per le lenti, esiste anche *l'aberrazione cromatica* (longitudinale e trasversale). Mediante lo studio del sistema ottico è possibile minimizzare alcune aberrazioni ma non tutte allo stesso modo. Di conseguenza spesso occorre stabilire un compromesso che privilegia una più forte diminuizione di alcune aberrazioni rispetto ad altre in base alla finalità dell'uso del sistema ottico.
L'ABERRAZIONE SFERICA NEL DIOTTRO SFERICO.

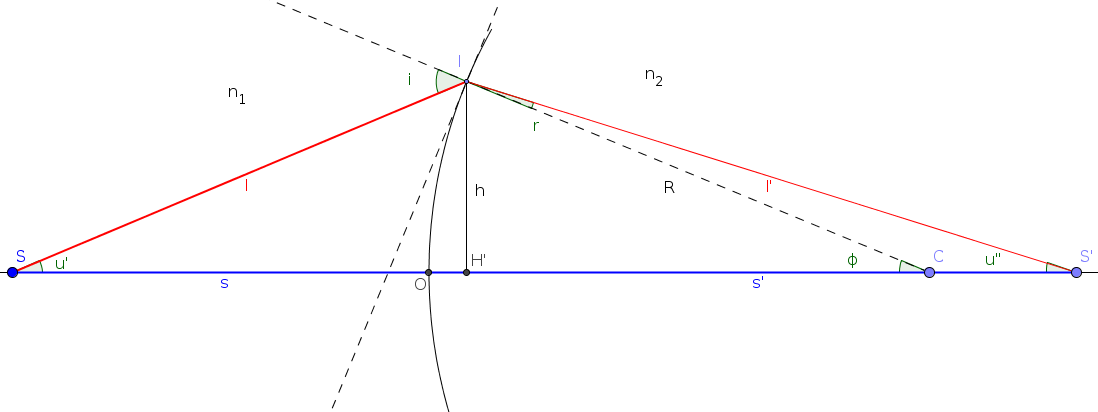
Consideriamo un diottro sferico. I cammini ottici L= SI + IS' e L'= SO + OS' non sono uguali (in approssimazione parassiale sono supposti uguali). La loro differenza dà luogo alle aberrazioni sferiche: $ΔL=L - L'=\left(n_1l+n_2l'\right)-\left(n_1s+n_2s'\right)$ Applicando il teorema del coseno ai triangoli SIC e CIS': $\begin{cases} l^2=R^2+(s+R)^2-2R\left(s+R\right)\cos \left(ϕ\right) \\ {l'}^2=R^2+(s'-R)^2-2R(s'-R)\cos \left(\pi-ϕ\right) \end{cases}$ Poichè h < R ( in approssimazione parassiale h ≪ R) cos ϕ può essere sviluppato in serie di Taylor: $\cos\left(ϕ\right)=\sqrt{1-\sin^2\left(ϕ\right)}=\sqrt{1-\left(\frac{h}{R}\right)^2}=1-\frac{h^2}{2R^2}-\frac{h^4}{8R^4}-\frac{h^6}{16R^6}- ...$ e i segmenti l e l' possono essere scritti (fermandosi ai primi tre termini dello sviluppo del coseno ): $\begin{cases} l=\sqrt{R^2+(s+R)^2-2R\left(s+R\right)\cos \left(ϕ\right)} = s \sqrt{\frac{R^2}{s^2}+\frac{\left(s+R\right)^2}{s^2}-2\frac{R}{s^2}\left(s+R\right)\cos\left({ϕ}\right)} \\l'=\sqrt{R^2+(s'-R)^2+2R(s'-R)\cos \left(ϕ\right)}= s' \sqrt{\frac{R^2}{{s'}^2}+\frac{\left({s'}-R\right)^2}{{s'}^2}+2\frac{R}{{s'}^2}\left({s'}-R\right)\cos\left({ϕ}\right)} \end{cases}⇒$ $⇒\begin{cases} l = s \sqrt{\frac{R^2}{s^2}+\frac{s^2}{s^2}+\frac{R^2}{s^2}+2\frac{sR}{s^2}-2\frac{Rs}{s^2}\cos\left({ϕ}\right)-2\frac{R^2}{s^2}\cos\left({ϕ}\right)} \\l' = {s'} \sqrt{\frac{R^2}{{s'}^2}+\frac{{s'}^2}{{s'}^2}+\frac{R^2}{{s'}^2}-2\frac{{s'}R}{{s'}^2}+2\frac{R{s'}}{{s'}^2}\cos\left({ϕ}\right)-2\frac{R^2}{{s'}^2}\cos\left({ϕ}\right)} \end{cases} ⇒ \begin{cases} l = s \sqrt{1+\frac{2R^2}{s^2}+\frac{2R}{s}-\frac{2R}{s}\left(1-\frac{h^2}{2R^2}-\frac{h^4}{8R^4}\right)-\frac{2R^2}{s^2}\left(1-\frac{h^2}{2R^2}-\frac{h^4}{8R^4}\right)} \\l'= {s'} \sqrt{1+\frac{2R^2}{{s'}^2}-\frac{2R}{{s'}}+\frac{2R}{{s'}}\left(1-\frac{h^2}{2R^2}-\frac{h^4}{8R^4}\right)-\frac{2R^2}{{s'}^2}\left(1-\frac{h^2}{2R^2}-\frac{h^4}{8R^4}\right)} \end{cases} ⇒$ $⇒ \begin{cases} l = s \sqrt{1+\frac{2R^2}{s^2}+\frac{2R}{s}-\frac{2R}{s}+\frac{h^2}{sR}+\frac{h^4}{4sR^3}-\frac{2R^2}{s^2}+\frac{h^2}{s^2}+\frac{h^4}{4s^2R^2}} \\l' = {s'} \sqrt{1+\frac{2R^2}{{s'}^2}-\frac{2R}{{s'}}+\frac{2R}{{s'}}-\frac{h^2}{{s'}R}-\frac{h^4}{4{s'}^2R^3}-\frac{2R^2}{{s'}^2}+\frac{h^2}{{s'}^2}+\frac{h^4}{4{s'}^2R^2}} \end{cases} ⇒ \begin{cases} l = s \sqrt{1+\frac{h^2}{sR}+\frac{h^4}{4sR^3}+\frac{h^2}{s^2}+\frac{h^4}{4s^2R^2}} \\l'= {s'} \sqrt{1-\frac{h^2}{{s'}R}-\frac{h^4}{4{s'}^2R^3}+\frac{h^2}{{s'}^2}+\frac{h^4}{4{s'}^2R^2}} \end{cases}⇒$ $⇒\begin{cases} l=s\sqrt{1+\frac{h^2}{s^2}\left(1+\frac{s}{R}\right)+\frac{h^4}{4s^2}\left(\frac{1}{R^2}+\frac{s}{R^3}\right)}=s\sqrt{1+\left[\frac{h^2\left(R+s\right)}{Rs^2}+\frac{h^4\left(R+s\right)}{4R^3s^2}\right]}\\ l'={s'}\sqrt{1+\frac{h^2}{{s'}^2}\left(1-\frac{{s'}}{R}\right)+\frac{h^4}{4{s'}^2}\left(\frac{1}{R^2}-\frac{{s'}}{R^3}\right)}={s'}\sqrt{1+\left[\frac{h^2\left(R-{s'}\right)}{R{s'}^2}+\frac{h^4\left(R-{s'}\right)}{4R^3{s'}^2}\right]} \end{cases}$ Poniamo : $\begin{cases} x= \frac{h^2\left(R+s\right)}{Rs^2}+\frac{h^4\left(R+s\right)}{4R^3s^2}\\ x'=\frac{h^2\left(R-{s'}\right)}{R{s'}^2}+\frac{h^4\left(R-{s'}\right)}{4R^3{s'}^2} \end{cases}$ Se h < R allora x e x' saranno minori di 1 e possiamo sviluppare in serie di Taylor $\sqrt{1+x}≃1+\frac{x}{2}-\frac{x^2}{8}+ ...$ , da cui: $\begin{cases} l=s\sqrt{1+x}≃s\left[1+\frac{x}{2}-\frac{x^2}{8}\right]=s\left[1+\frac{1}{2}\left( \frac{h^2\left(R+s\right)}{Rs^2}+\frac{h^4\left(R+s\right)}{4R^3s^2}\right)-\frac{1}{8}\left( \frac{h^2\left(R+s\right)}{Rs^2}+\frac{h^4\left(R+s\right)}{4R^3s^2}\right)^2\right]\\ l'=s'\sqrt{1+x'}≃s\left[1+\frac{x'}{2}-\frac{{x'}^2}{8}\right] =s'\left[1+\frac{1}{2}\left(\frac{h^2\left(R-{s'}\right)}{R{s'}^2}+\frac{h^4\left(R-{s'}\right)}{4R^3{s'}^2}\right)-\frac{1}{8}\left(\frac{h^2\left(R-{s'}\right)}{R{s'}^2}+\frac{h^4\left(R-{s'}\right)}{4R^3{s'}^2}\right)^2\right]\end{cases}$ sviluppando il quadrato teniamo solo i termini con massimo h⁴: $\begin{cases} l=s\left[1+\frac{h^2\left(R+s\right)}{2Rs^2}+\frac{h^4\left(R+s\right)}{8R^3s^2}-\frac{h^4\left(R+s\right)^2}{8R^2s^4}\right]⇒l-s=s\left[\frac{h^2\left(R+s\right)}{2Rs^2}+\frac{h^4\left(R+s\right)}{8R^3s^2}-\frac{h^4\left(R+s\right)^2}{8R^2s^4}\right]\\ l'=s'\left[1+\frac{h^2\left(R-s'\right)}{2R{s'}^2}+\frac{h^4\left(R+s'\right)}{8R^3{s'}^2}-\frac{h^4\left(R+s'\right)^2}{8R^2{s'}^4}\right]⇒l'-s'=s'\left[\frac{h^2\left(R-s'\right)}{2R{s'}^2}+\frac{h^4\left(R+s'\right)}{8R^3{s'}^2}-\frac{h^4\left(R+s'\right)^2}{8R^2{s'}^4}\right] \end{cases}$ Possiamo adesso avere una stima delle aberrazioni sferiche: $ΔL=n_1\left(l-s\right)+n_2\left(l'-s'\right)=n_1s\left[\frac{h^2\left(R+s\right)}{2Rs^2}+\frac{h^4\left(R+s\right)}{8R^3s^2}-\frac{h^4\left(R+s\right)^2}{8R^2s^4}\right]+n_2s'\left[\frac{h^2\left(R-s'\right)}{2R{s'}^2}+\frac{h^4\left(R+s'\right)}{8R^3{s'}^2}-\frac{h^4\left(R+s'\right)^2}{8R^2{s'}^4}\right]=$ $=\frac{h^2}{2}\left[\left(\frac{n_1}{s}+\frac{n_2}{s'}\right)-\left(\frac{n_2-n_1}{R}\right)\right]-\frac{h^4}{8}\left[\frac{n_1}{s}\left(\frac{1}{s}+\frac{1}{R}\right)^2+\frac{n_2}{s'}\left(\frac{1}{s'}-\frac{1}{R}\right)^2\right]$ Ora la formula di Gauss per il diottro sferico è : $\frac{n_1}{s}+\frac{n_2}{s'}=\frac{n_2-n_1}{R}$ , e sostituendo, l'aberrazione sferica si riduce a: $ΔL=\frac{h^4}{8}\left[\frac{n_1}{s}\left(\frac{1}{s}+\frac{1}{R}\right)^2+\frac{n_2}{s'}\left(\frac{1}{s'}-\frac{1}{R}\right)^2\right]=ch^4$ Si può osservare che che l'aberrazione sferica è proporzionale alla quarta potenza dell'apertura h del sistema (c è un parametri caratteristico del sistema ottico).
L'ABERRAZIONE SFERICA NELLO SPECCHIO SFERICO.

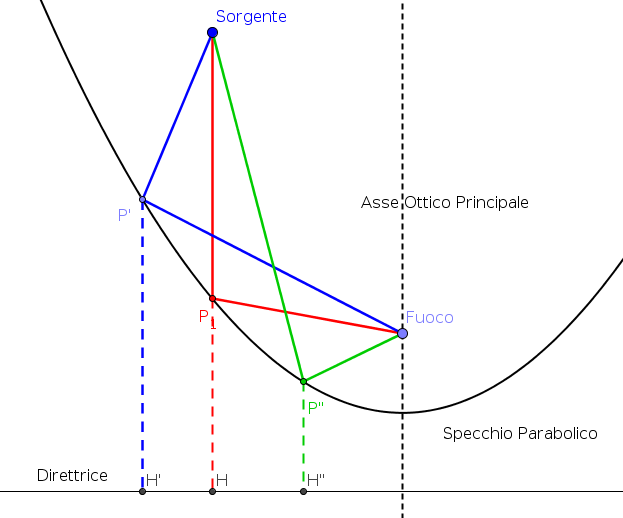
LO SPECCHIO PARABOLICO E IPERBOLICO. Supponiamo che tre raggi sono emessi dalla sorgente S, che raggiungano lo specchio parabolico e che, riflessi, passino per il fuoco. Solo la riflessione del raggio che incide in P è fisicamente possibile. Infatti, per le proprietà della parabola sono uguali le distanze:

\begin{cases} \widebar{P'H'}=\widebar{P'F} \\ \widebar{PH}=\widebar{PF}\\ \widebar{P''H''}=\widebar{P''F} \end{cases}

I cammini ottici sono

\begin{cases} L_1=\widebar{P'F}+\widebar{SP'} = \widebar{P'H'}+\widebar{SP'}\\ L_2=\widebar{PF}+\widebar{SP}=\widebar{PH}+\widebar{SP}\\ L_3= \widebar{P''F}+\widebar{SP''} =\widebar{P''H''}+\widebar{SP''}\end{cases}

La distanza più piccola tra un punto e una retta è lungo la perpendicolare per quel punto. Allora L₁ è il minimo cammino ottico ed è l'unico possibile per il Principio di Fermat.

"Tutti i raggi paralleli all'asse ottico principale, quando riflessi da uno specchio parabolico, passano per il fuoco"

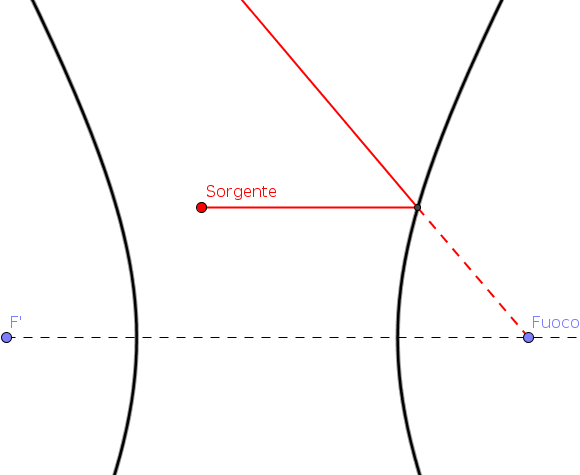
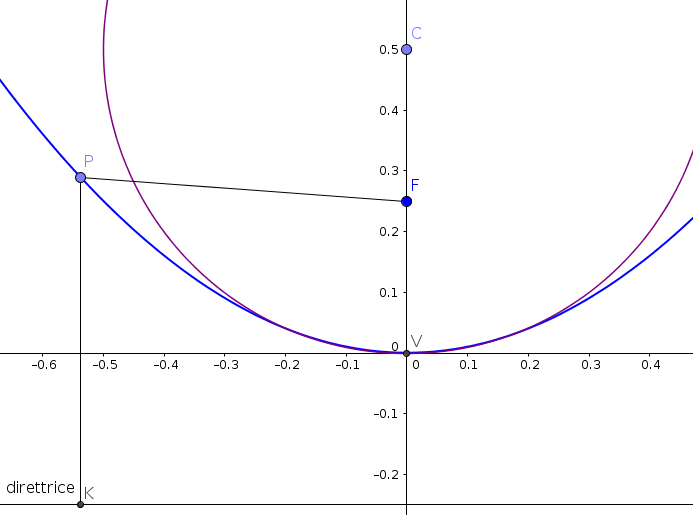
È possibile anche produrre uno specchio iperbolico ma in quel caso:

"I prolungamenti di tutti i raggi paralleli all'asse ottico principale, quando riflessi da uno specchio iperbolico, passano per il fuoco"

Il fuoco di uno specchio iperbolico è virtuale, quello di uno specchio parabolico è reale.

SPECCHI SFERICI E SPECCHI PARABOLICI
La superficie di uno specchio sferico è quella di una calotta sferica. Sotto certe approssimazioni uno specchio sferico, di raggio doppio della distanza focale, può approssimare uno specchio parabolico.

Una circonferenza con centro nell'asse delle ordinate è descritta dalla funzione:

$y(x)=R±\sqrt{R^2-x^2}$ La semicirconferenza passante per l'origine dalla funzione: $y(x)=R-\sqrt{R^2-x^2}$ Sviluppiamo in serie di Taylor la funzione nell'intorno dell'origine (è una funzione pari e quindi lo sviluppo presenterà solo termini pari): $y(x)=y(0)+\frac{y''(0)}{2!}x^2+\frac{y''''(0)}{4!}x^4+...$ Le derivate: $y'(x)=-\frac{1}{2\sqrt{R^2-x^2}}\cdot \left(-2x\right)=\frac{x}{\sqrt{R^2-x^2}}$ $y''(x)=\frac{1}{\sqrt{R^2-x^2}}+x\left[-\frac{1}{2}\cdot \frac{-2x}{\sqrt{\left(R^2-x^2\right)^3}}\right]=\frac{R^2-x^2+x^2}{\sqrt{(R^2-x^2)^3}}=\frac{R^2}{\sqrt{(R^2-x^2)^3}}$ $y'''(x)=R^2\left(-\frac{3}{2}\right)(R^2-x^2)^{-3/2-1}\cdot(-2x)=\frac{3R^2x}{\sqrt{(R^2-x^2)^5}}$
$y''''(x)=3R^2\left[\frac{1}{\sqrt{(R^2-x^2)^5}}-\frac{5x}{2}(R^2-x^2)^{-5/2-1}\cdot (-2x)\right]=3R^2\left(\frac{1}{\sqrt{(R^2-x^2)^5}}+\frac{5x^2}{\sqrt{(R^2-x^2)^7}}\right)$ In x=0: $\begin{cases} y(0)=0 \\ y''(0)=\frac{1}{R}\\y''''(0)=\frac{3}{R^3} \end{cases}$ Sostituendo nello sviluppo: $y(x)=0+\frac{1}{R}\frac{x^2}{2}+\frac{3}{R^3}\frac{x^4}{24}+...=\frac{x^2}{2R}+\frac{1}{8}\frac{x^4}{R^3}+...$ L'equazione di una parabola con vertice nell'origine è: $y_p(x)=\frac{x^2}{4f}$ con f ordinata del fuoco. Quindi se R= 2f e se $\frac{x^2}{2R}≫\frac{x^4}{8R^3}⇒x^2≪4R^2⇒x≪2R$ allora è possibile sostituire uno specchio parabolico con uno specchio sferico.
La differenza tra il cammino ottico in uno specchio parabolico e in uno specchio sferico con R=2f è detta aberrazione sferica nello specchio sferico.
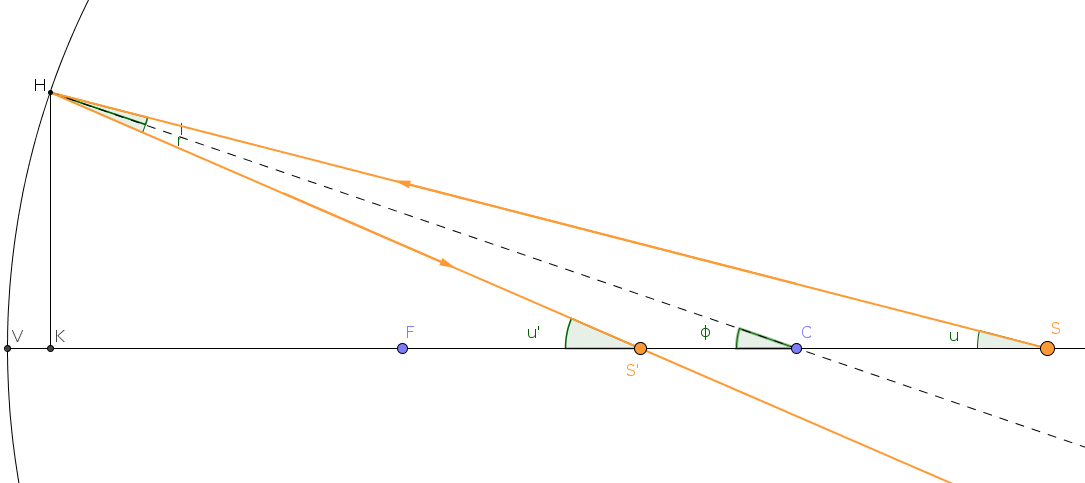
Dalla figura questa differenza è : $ΔL≃\widebar{AC}-\widebar{A'F}$ con $y(x)-y_p(x)=\frac{x^2}{2R}+\frac{1}{8}\frac{x^4}{R^3}+...-\frac{1}{R}\frac{x^2}{2}=\frac{1}{8}\frac{x^4}{R^3}+...$ Si può osservare che che l'aberrazione sferica è proporzionale alla quarta potenza dell'apertura x dello specchio. L'EQUAZIONE DEI PUNTI CONIUGATI S è una sorgente e S' è la sua immagine. Dalla figura (Teorema angolo esterno) : $u'=ϕ+r$ e $ϕ=i+u$ Ma i = r, da cui: $u+u'=ϕ+r+ϕ-i=2ϕ$

Dalla definizione di tangente: $\begin{cases} \tan\left({u}\right)=\frac{\widebar{HK}}{\widebar{KS}} \\ \tan\left({u'}\right)=\frac{\widebar{HK}}{\widebar{KS'}}\\\tan\left({ϕ}\right)=\frac{\widebar{\widebar{HK}}}{\widebar{KC}} \end{case$ In approssimazione parassiale : $\begin{cases} \widebar{KS}≃\widebar{VS}=p \\ \widebar{KS'}≃\widebar{VS'}=q\\\widebar{KC}≃\widebar{VC}=R \end{cases} \qquad \begin{cases}\tan\left({u}\right)≃u \\\tan\left({u'}\right)≃u'\\\tan\left({ϕ}\right)≃ϕ \end{cases$
Da cui, sostituendo: $\frac{\widebar{HK}}{p}+\frac{\widebar{HK}}{q}=2\frac{\widebar{HK}}{R}$ l'equazione dei punti coniugati: $\frac{1}{p}+\frac{1}{q}=\frac{1}{f}$ con f= R/2
In approssimazione parassiale inoltre si ha che: $\begin{cases} h_o=\widehat{i }\cdot p \\ h_i = \widehat{r} \cdot q \end{cases}$ Definiamo ingrandimento lineare G: $G= \frac{h_i}{h_o}$ e lo vogliamo negativo se l'immagine è capovolta e positivo se è diritta. Allora, in approssimazione parassiale,: 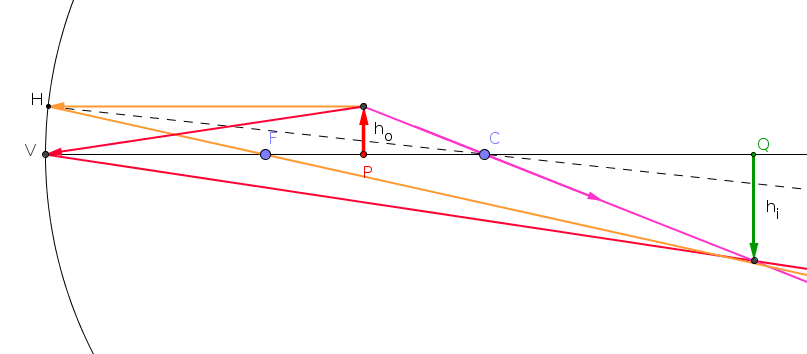$G= -\frac{q}{p}$	Formazione dell'immagine in approssimazione parassiale
Formazione dell'immagine in specchi di grande rapporto d'apertura (D/f)

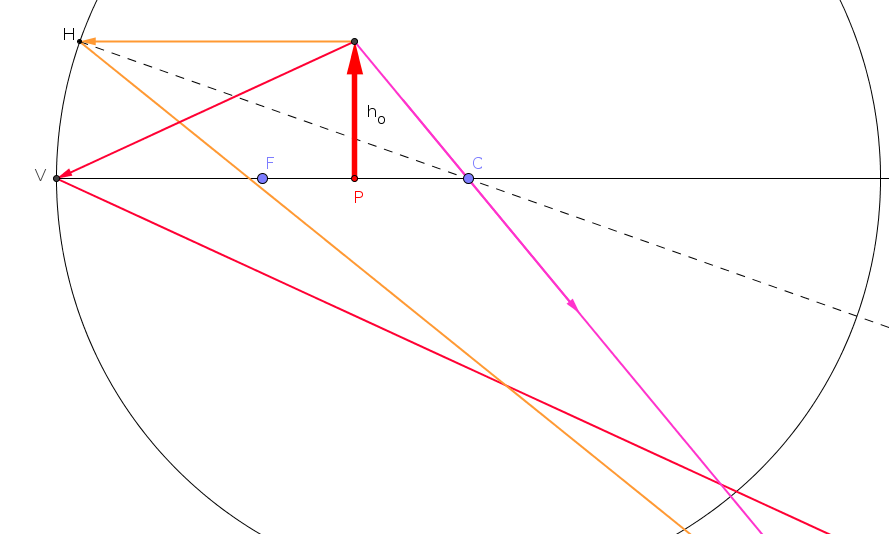LE ALTRE ABERRAZIONI GEOMETRICHE O MONOCROMATICHE

Se la sorgente è fuori asse le cose si complicano ma sulla base della precedente analisi le aberrazioni conseguenti possono essere stimate perché sono proporzionali alla quarta potenza della distanza fra due raggi di luce uno centrato e uno non centrato.
Nella figura la luce proviene da un punto P non più posto nell'asse ottico principale ma in un asse ottico secondario appartenente al piano passante per centro di curvatura C e per il centro di simmetria O del sistema ottico (piano di simmetria)
Esaminiamo tre cammini ottici da P a P':

L(PBP') passante per il punto B e per il centro di curvatura (non viene rifratto dal sistema ottico);
L(PQP') passante per un punto Q;
L(POP') passante per il centro di simmetria O.

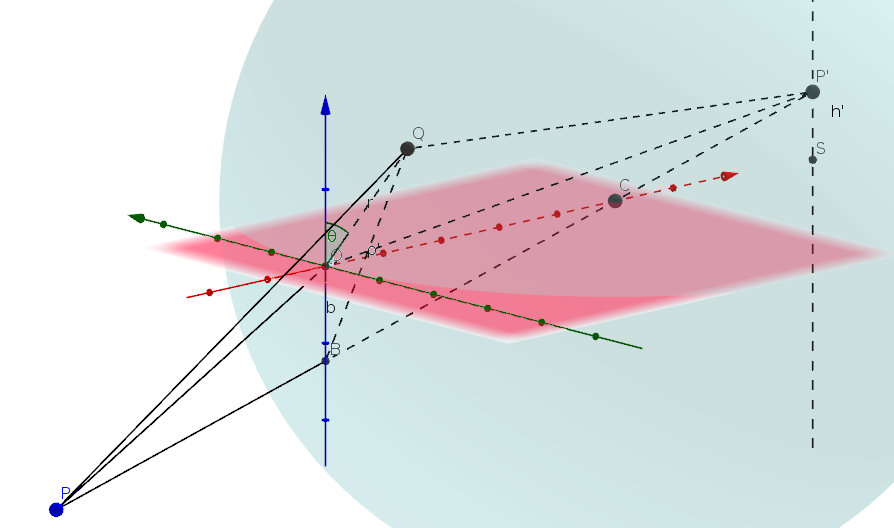La differenza dei cammini ottici PQP' e PBP' dà luogo alla aberrazione per il punto Q:

ΔL(Q)=L(PQP') - L(PBP')=c(BQ)^4=cρ^4

La differenza dei cammini ottici POP' e PBP' dà luogo alla aberrazione per il punto O:

ΔL(O)=L(POP') - L(PBP')=c(BO)^4=cb^4

La differenza delle due aberrazioni è:

ΔL=ΔL(Q) - ΔL(O) = c\left(ρ^4-b^4\right)

Applicando il teorema del coseno al triangolo OBQ:

ρ^2=r^2+b^2+2rb\,\cos\left({θ}\right)

I triangoli OBC e SP'C sono simili e si deduce che che b è proporzionale ad h', l'altezza dell'immagine:

b∝h'

Sostituendo ρ² e b in ΔL in generale possiamo scrivere:

ΔL=c\left(ρ^4-b^4\right)=c\left[\left(r^2+k^2{h'}^2+2r{h'}\,\cosθ\right)^2-k^4{h'}^4\right]=C_{40}r^4+C_{31}h'r^3cosθ+C_{22}{h'}^2r^2cos^2θ+C_{20}{h'}^2r^2+C_{11}{h'}^3r\,cosθ

dove:

gli indici dei coefficienti C_ij indicano gli esponenti di r e cosθ;
h' è la posizione dell'immagine;
r è la massima apertura della superficie rifrangente;
cosθ indica lo spostamento dal piano di simmetria.

Ogni termine dà luogo ad un diverso tipo di aberrazione geometrica o monocromatica:

il termine in r⁴ è responsabile dell'aberrazione sferica;
il termine in h'r³cosθ è responsabile dell'aberrazione del coma;
il termine h'²r²cos²θ è responsabile dell'aberrazione di astigmatismo;
il termine h'²r² è responsabile dell'aberrazione di curvatura di campo;
il termine h'³rcosθ è responsabile dell'aberrazione di distorsione.

SPOT DIAGRAMS

Per giudicare la qualità di immagine di un sistema ottico occorre calcolare e definire la natura e la distribuzione delle aberrazioni nei dintorni del piano focale e l'aberrazione globale sarà in generale data dalla somma di più tipi di aberrazione. La maniera più immediata ed intuitiva per rappresentare l’entità e la composizione delle aberrazioni è lo spot diagram il quale simula la forma, la dimensione e la distribuzione delle “macchie di luce” nella superficie dell’immagine (questa distribuzione è detta Point Spread Function psf). Utilizzando le equazioni dell’ottica geometrica e mediante software vengono determinati i percorsi di ipotetici fasci di raggi luminosi che giungendo dall’infinito attraversano il sistema di lenti e specchi fino ad arrivare al piano focale. In particolare vengono analizzati:

i fasci paralleli all’asse ottico in prossimità di quest’ultimo ed alla periferia del piano focale
i fasci inclinati rispetto all’asse ottico
i fasci di luce di differente lunghezza d’onda per valutare l’entità delle aberrazioni cromatiche

Muovendo avanti e indietro il piano focale (intrafocale, il piano focale è avvicinato, extrafocale, il piano focale è allontanato) viene analizzata la posizione di miglior fuoco in funzione della distanza dall’asse ottico.

In figura (da a ad e, da intrafocale a extrafocale) uno spot diagram di un sistema ottico con aberrazioni trascurabili.

Aberrazione sferica. Se è presente aberrazione sferica l'anello esterno dell'immagine in intrafocale (sinistra) e' piu' diffuso, mentre quello esterno extrafocale (destra) e' molto piu' luminoso degli altri se l'aberrazione sferica è negativa (al contrario per l'aberrazione sferica positiva).

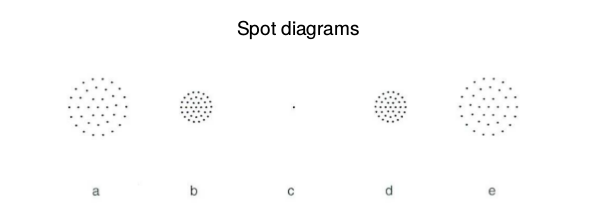Sistema ottico con aberrazioni trascurabili

Spot diagrams con aberrazione sferica positiva

Aberrazione sferica negativa nelle lenti

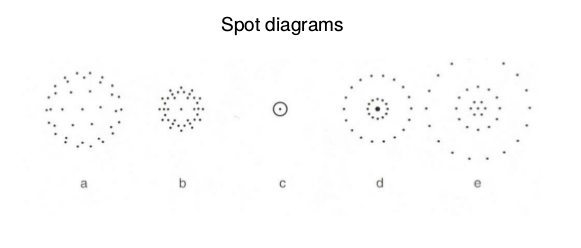Aberrazione sferica negativa

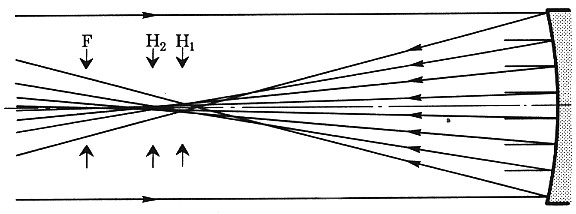Aberrazione sferica negativa negli specchi

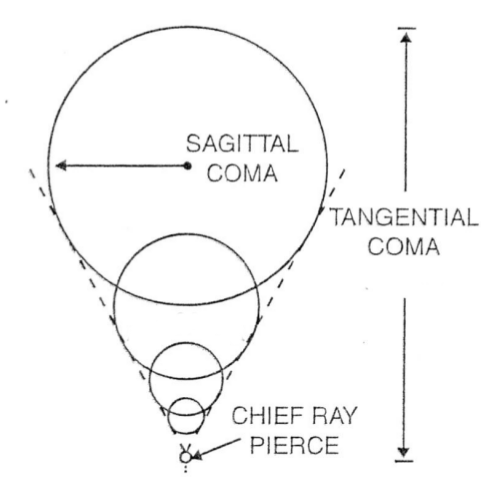
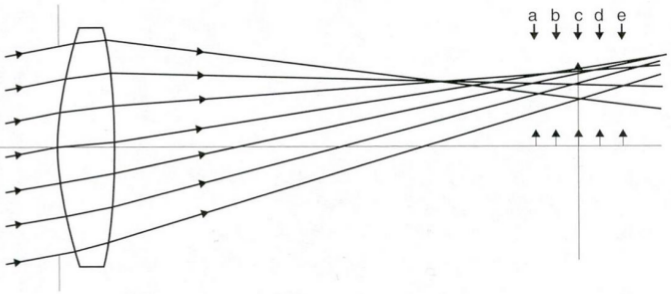La coma

Coma. Si verifica per oggetti che si trovano fuori asse. I raggi emessi incidono obliqui sull’apertura del sistema ottico e l’intersezione dei raggi focalizzati, rispetto all’asse ottico, non è simmetrica come per la sferica. Si produce un’immagine a forma di cometa, con il nucleo più luminoso e la coda più sfumata.
La larghezza della coma è detta coma sagittale mentre la sua altezza è detta coma tangenziale.

La coma

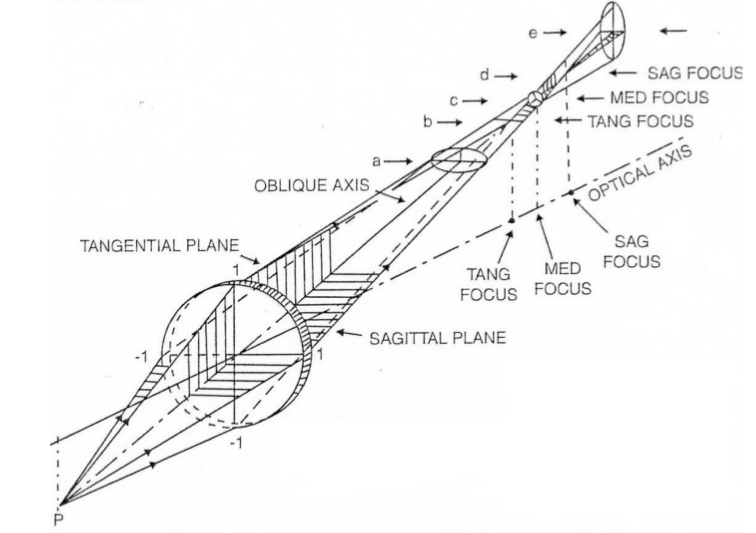
Astigmatismo. Si verifica quando uno specchio sferico o parabolico presenta curvature diverse lungo la direzione orizzontale e verticale. I raggi che incidono fuori asse sullo specchio in un piano verticale vanno a fuoco prima di quelli che incidono su un piano orizzontale. L'immagine di una sorgente puntiforme in questi due fuochi apparirà allungata in senso orizzontale (intrafocale) o in senso verticale (extrafocale). L'osservatore cercherà il miglior compromesso tra le 2 posizioni, col risultato che la sorgente puntiforme apparirà come una piccola croce.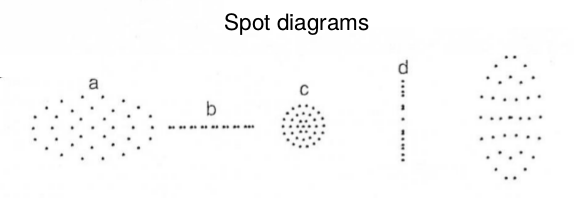

L'astigmatismo

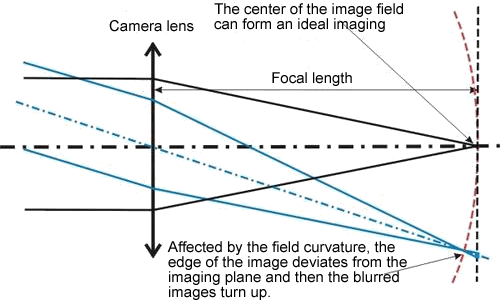
Curvatura di campo. I raggi provenienti da un oggetto fuori asse che attraversano il sistema ottico, non vanno a fuoco su un piano, ma su una superficie curva. Il fuoco migliore, per raggi provenienti da distanze diverse, si forma su piani diversi. Quando la sorgente è messa a fuoco, spostandoci sul piano focale, si ottengono gli spot diagrams.

Spot diagrams sul piano focale

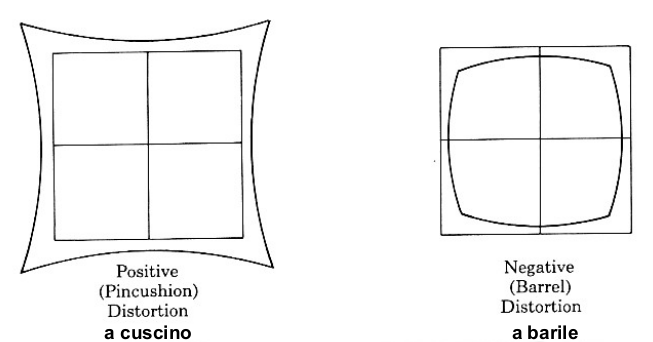
Distorsione. Anche la distorsione è un'aberrazione fuori asse. Essa influisce principalmente sulla scala, cioè sulle distanze reciproche tra punti nell’immagine che sono espanse (distorsione positiva a “cuscino”) o compresse (distorsione negativa a “barilotto” come nell’immagine) rispetto alle distanze nell’oggetto. La scala dell’immagine e l’ingrandimento non è costante, ma varia con la distanza dall’asse ottico.