BLOCCHI, FILI E CARRUCOLE

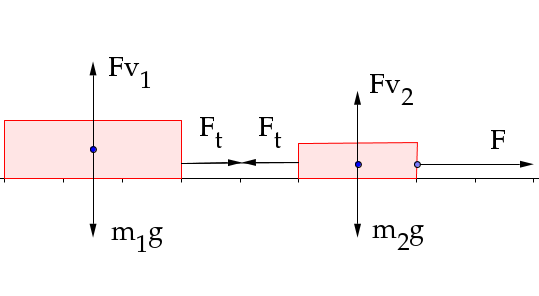
Due blocchi sono collegati con un filo e sono posti su un piano orizzontale senza attrito. Un forza li tira. Determinare l'accelerazione del sistema e la tensione del filo. Scelto l'asse delle ascisse parallelo al piano, le equazioni di Newton per i due blocchi sono:
Blocco m₂: ${\begin{matrix} a s s e x : & F - F_{t} = m_{2} a \\ a s s e y : & F_{v 2} - m_{2} g = 0 \end{matrix}$	Blocco m₁: ${\begin{matrix} a s s e x : & F_{t} = m_{1} a \\ a s s e y : & F_{v 1} - m_{1} g = 0 \end{matrix}$
Sommando le equazioni relative all'asse x si trova l'accelerazione: $F - F_{t} + F_{t} = m_{1} a + m_{2} a \to F = (m_{1} + m_{2}) a \to a = \frac{F}{m_{1} + m_{2}}$ Da cui la tensione del filo: $T = m_{1} a = \frac{m_{1}}{m_{1} + m_{2}} F$
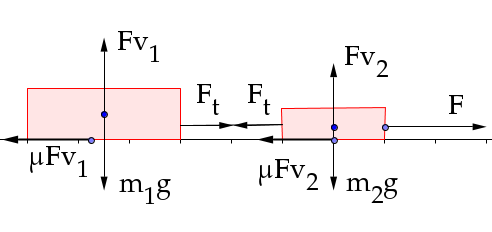
Due blocchi sono collegati con un filo e sono posti su un piano orizzontale con uguale attrito. Una forza li tira. Determinare l'accelerazione del sistema e la tensione del filo.
Equazioni di Newton per i due blocchi:
Blocco m₂: ${\begin{matrix} a s s e x & F - μ F v_{2} - F_{t} = m_{2} a \\ a s s e y & F v_{2} - m_{2} g = 0 \end{matrix}$	Blocco m₁: ${\begin{matrix} a s s e x & F_{t} - μ F v_{1} = m_{1} a \\ a s s e y & F v_{1} - m_{1} g = 0 \end{matrix}$
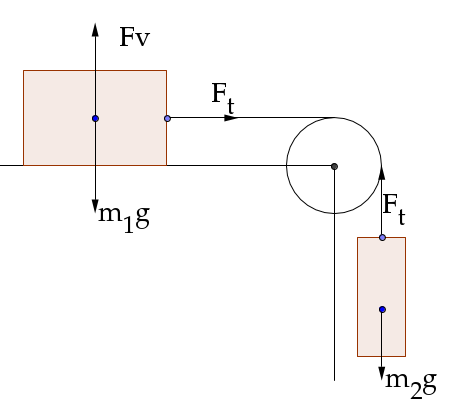
Sommando le equazioni relative all'asse x si trova l'accelerazione: $F - μ m_{2} g - F_{t} + F_{t} - {μ m}_{1} g = m_{1} a + m_{2} a \to F - μ (m_{1} + m_{2}) g = (m_{1} + m_{2}) a \to a = \frac{F - μ (m_{1} + m_{2}) g}{m_{1} + m_{2}}$ Da cui anche la tensione: $F_{t} = {μ m}_{1} g + m_{1} a = μ m_{1} g + m_{1} \frac{F - μ (m_{1} + m_{2}) g}{m_{1} + m_{2}} = m_{1} \frac{μ m_{1} g + μ m_{2} g + F - μ m_{1} g - μ m_{2} g}{m_{1} + m_{2}} = \frac{m_{1}}{m_{1} + m_{2}} F$
Due blocchi sono collegati con un filo come in figura e sono liberi di muoversi. Determinare l'accelerazione del sistema e la tensione del filo in assenza d'attrito. L'asse delle ascisse per il blocco 1 è scelto orizzontale verso destra, per il blocco 2 è scelto verticale verso il basso. In questo modo le accelerazioni saranno concordi. Le equazioni di Newton applicate ai due blocchi sono:
Blocco 1: ${\begin{matrix} a s s e x & F_{t} = m_{1} a \\ a s s e y & F_{v} - m_{1} g = 0 \end{matrix}$	Blocco 2: ${\begin{matrix} a s s e x & m_{2} g - F_{t} = m_{2} a \\ a s s e y & 0 = 0 \end{matrix}$
Sommando le due equazioni relative all'asse x: $F_{t} + m_{2} g - F_{t} = m_{1} a + m_{2} a \to m_{2} g = (m_{1} + m_{2}) a \to a = \frac{m_{2} g}{m_{1} + m_{2}}$ Da cui la tensione del filo: $F_{t} = m_{1} a = \frac{m_{1} m_{2}}{m_{1} + m_{2}} g$
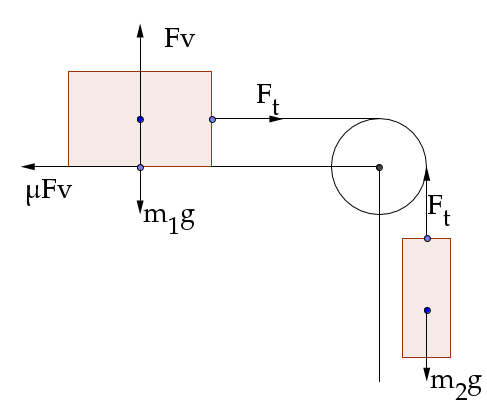
Due blocchi sono collegati con un filo come in figura e sono liberi di muoversi. Determinare l'accelerazione del sistema e la tensione del filo in presenza d'attrito . L'asse delle ascisse per il blocco 1 è scelto orizzontale verso destra e per il blocco 2 è scelto verticale verso il basso. In questo modo le accelerazioni saranno concordi. Le equazioni di Newton applicate ai due blocchi sono:
Blocco 1: ${\begin{matrix} a s s e x & F_{t} - {μ m}_{1} g = m_{1} a \\ a s s e y & F_{v} - m_{1} g = 0 \end{matrix}$	Blocco 2: ${\begin{matrix} a s s e x & m_{2} g - F_{t} = m_{2} a \\ a s s e y & 0 = 0 \end{matrix}$
Sommando le due equazioni relative all'asse x: $F_{t} - μ m_{1} g + m_{2} g - F_{t} = m_{1} a + m_{2} a \to m_{2} g - μ m_{1} g = (m_{1} + m_{2}) a \to a = \frac{m_{2} - μ m_{1}}{m_{1} + m_{2}} g$ Da cui la tensione del filo: $F_{t} = m_{1} a + μ m_{1} g = m_{1} \cdot \frac{m_{2} - μ m_{1}}{m_{1} + m_{2}} g + μ m_{1} g = \frac{m_{2} - μ m_{1} + μ m_{1} + μ m_{2}}{m_{1} + m_{2}} \cdot m_{1} g = \frac{m_{2} m_{1} (1 - μ)}{m_{1} {+ m}_{2}} g$