I TEOREMI DEL CALCOLO DIFFERENZIALE

Determinare per quale valore del parametro a, se esiste, la funzione: $f (x) =$ ${\begin{matrix} 2 x^{2} + (a + 3 b - 2) x + (2 a - b - 1) x < 0 \\ 1 + \ln (1 - x + 3 x^{2}) x \geq 0 \end{matrix}$ è derivabile in x=0.
Data la curva di equazione: $f (x) = {\begin{matrix} x^{2} + b x - 4 + c se x < 0 \\ \frac{a x - 2}{x + 3} se x \geq 0 \end{matrix}$ individua, senza risolvere l’equazione f'(x)= 0 i valori dei parametri a, b e c per cui nell’intervallo [-1; 2] è garantita l’esistenza di un punto in cui la retta tangente alla curva è orizzontale.
Determinare i valori di a e b affinchè la funzione: $f (x) = {\begin{matrix} a e^{x^{2} - 4} se x \geq 2 \\ 1 + b x^{2} + {(x - 2)}^{3} se x < 2 \end{matrix}$ sia derivabile in x=2.
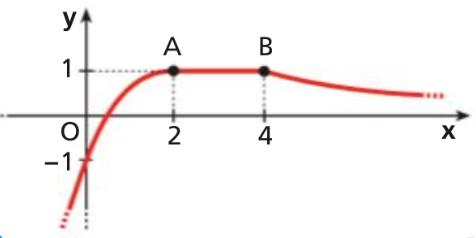
Date le due curve di equazione $f (x) = e^{x^{2} - 4 x + 4}$ e $g (x) = \cos (x - 2)$ dimostra che esiste almeno un valore c interno all’intervallo [0; 4] per il quale le rette tangenti alle curve, rispettivamente nei punti (c; f (c)) e (c; g (c)), sono parallele
Considera il grafico della funzione $f (x) = x^{3} - 4 x + a con a \in ℝ$ passante per il punto A(1; 3). Dimostra, mediante il teorema di Lagrange, che esiste almeno una retta tangente al grafico in un punto D di ascissa interna all’intervallo [-2; 1], parallela alla congiungente i punti A e B della curva, con B di ascissa -2. Determina l’area del triangolo BAD.

La funzione rappresentata in figura è costituita da un arco di parabola di vertice A, dal segmento AB e da un arco di iperbole equilatera riferita ai propri asintoti e passante per B.
1. Determina l’espressione analitica della funzione.
2. Verifica l’applicabilità del teorema di Lagrange in [0; 4] e determina il punto garantito dal teorema.

Data la funzione f ( x ) = { k e x − 1 se x < 1 k ( x 2 − x ) + k se x ≥ 1 f( x )= left lbrace stack{k e^{x-1} ~"se"~ x<1# k(x^2-x)+k ~"se"~ x ge 1} right none
1. dimostra che f(x) è continua e derivabile in R;
2. trova il valore di k in modo che la tangente al grafico della funzione nel suo punto di ascissa 1 abbia coefficiente angolare uguale a -1 e rappresenta graficamente f(x);
3. applica il teorema di Lagrange agli intervalli [1;4] e [0;2] nelle ipotesi del punto b